Question

помогите пожалуйста!
1) радиус шара равен √13. найти площадь поверхности шара.
2) объем шара равен 2500π. найти радиус шара.
3)площадь сечения шара равна 64π. найти площадь поверхности шара, если расстояние от центра до цента сечения равно 9.

Answer 1

Ответ:

1) Площадь поверхности шара равна 52π кв.ед.

2) радиус шара равен $5\sqrt[3]{15}$  ед.

3) площадь поверхности шара  580π кв.ед.

Объяснение:

1) Радиус шара равен $R= \sqrt{13}$ ед.

Найдем площадь поверхности шара по формуле:

$S =4\pi R^{2} ,$    где   R - радиус шара

$S =4\pi \cdot(\sqrt{13} )^{2} =4\pi \cdot13=52\pi$  кв.ед.

2) Объем шара равен 2500π куб. ед. Надо найти радиус шара.

Объем шара определяется по формуле :

$V =\dfrac{4}{3} \pi R^{3} , R -$  радиус шара.

Тогда получим

$\dfrac{4}{3} \pi R^{3} =2500\pi |:\pi ;\\\\\dfrac{4}{3} R^{3} =2500|\cdot 3;\\\\4R^{3} =7500;\\\\R^{3} =7500:4;\\\\R^{3} =\dfrac{75\cdot 100}{4} ;\\\\R^{3} =75\cdot25;\\\\R^{3} =125\cdot15;\\\\R=\sqrt[3]{125\cdot15} ;\\\\R= 5\sqrt[3]{15} .$

Значит, радиус шара равен $5\sqrt[3]{15}$  ед.

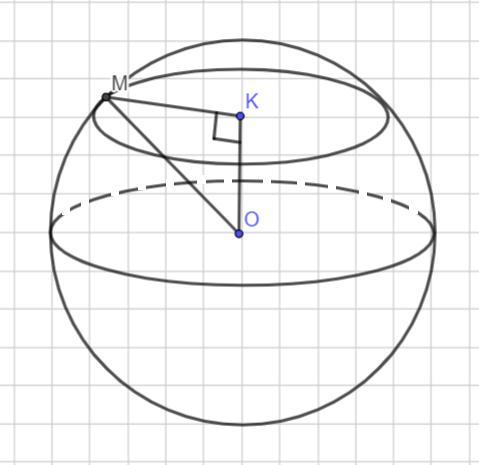
3) Площадь сечения шара равна 64 π кв. ед. . Любое сечение шара - это круг. Тогда площадь круга равна 64 π кв. ед. Найдем радиус сечения шара .

Площадь круга определяется по формуле:

$S =\pi r^{2} ;\\\pi r^{2}=64\pi |:\pi ;\\r^{2} =64;\\r=8$

Тогда МК =8 ед. Рассмотрим  Δ ОКМ - прямоугольный . Ок = 9 ед.

Найдем радиус шара  ОМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$OM ^{2} =OK^{2} +MK^{2} ;\\OM =\sqrt{OK^{2} +MK^{2}} ;\\OM= \sqrt{8^{2} +9^{2} } =\sqrt{64+81} =\sqrt{145}$

Тогда площадь поверхности шара

$S =4\pi R^{2};\\S =4\pi \cdot( \sqrt{145} )^{2} =4\pi \cdot145=580\pi$  кв. ед.

#SPJ1