Предмет: Математика,
автор: yyuiffli
Найди значение выражения если угол а острый и тангенс угла А равен 2
Приложения:
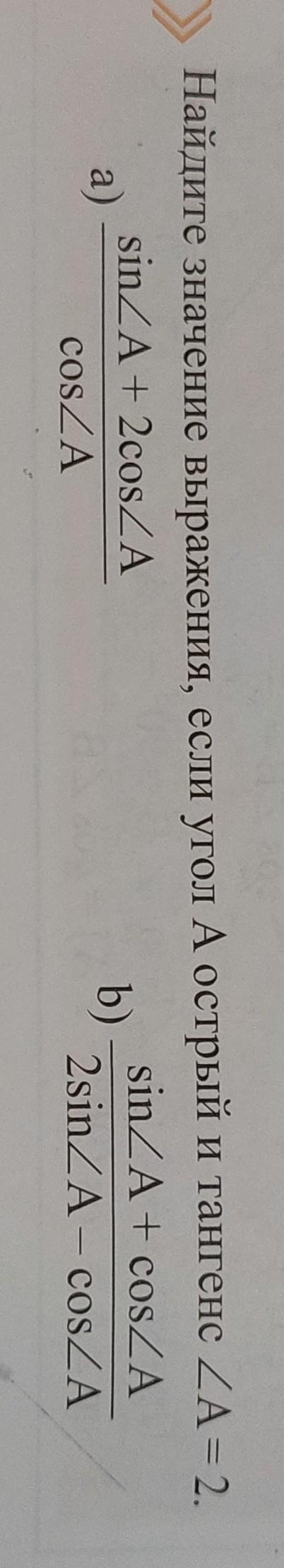
Ответы
Автор ответа:
12
Ответ:
a)
b)
Пошаговое объяснение:
По условию tg ∠A = 2 и ∠A - острый.
Воспользуемся формулой
Найдем значение выражения
а)
b)
Разделим числитель и знаменатель дроби на
#SPJ1
Похожие вопросы
Предмет: Другие предметы,
автор: саша2564
Предмет: Английский язык,
автор: nik234145336636
Предмет: Окружающий мир,
автор: инна326
Предмет: Математика,
автор: Mishania2008mg
Предмет: Алгебра,
автор: stepanlysenko21