Question

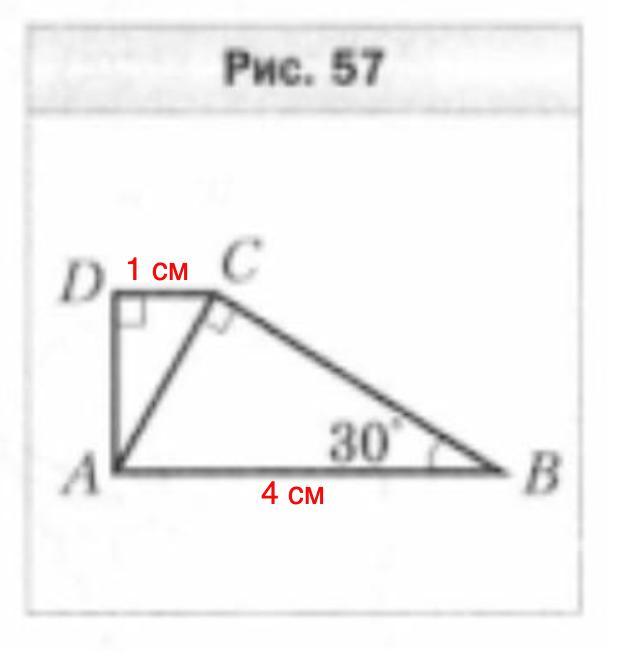
Hа рисунке 57 angle ACB=90^ , angle ADC=90^ , angle ABC=30^ prime ,Ha tilde n - дите угол ACD, если AB = 4cx , CD = 1CM. На

. В треугольнике АВС известно, что angle C=90 , angle A=60^ Биссек триса угла А пересекает ка тет ВС в точке К. Найдите ВК, если АК-СК
СРОЧНО ПОЖАЛУЙСТА!!!​

Answer 1

Ответ:

147. Угол ACD равен 60°;

148. BK = 16 см.

Объяснение:

Требуется найти:

147. Угол ACD;

148. BK.

147.

Дано: ∠АСВ = 90°;

∠ADC = 90°;

∠ABC = 30°;

АВ = 4 см; CD = 1 см.

Найти: ∠ACD.

Решение:

1. Рассмотрим ΔАСВ - прямоугольный.

∠АВС = 30°.

• Катет, лежащий против угла 30°, равен половине гипотенузы.

⇒ АС = АВ : 2 = 4 : 2 = 2 (см)

2. Рассмотрим ΔADC - прямоугольный.

АС = 2 см - гипотенуза;

DC = 1 см - катет.

• Если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то он лежит против угла в 30°.

⇒ ∠DAC = 30°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ACD = 90° - 30° = 60°.

Угол ACD равен 60°.

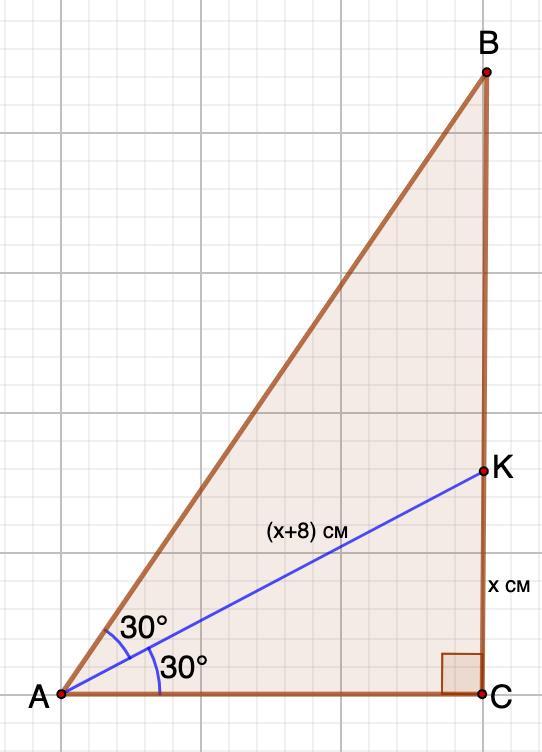
148.

Дано: ΔАВС - прямоугольный;

∠С = 90°; ∠А = 60°;

АК - биссектриса;

АК - СК = 8 см.

Найти: ВК.

Решение:

1. Рассмотрим ΔАВС - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠В = 90° - ∠А = 90° - 60° = 30°

2. Рассмотрим ΔАКС - прямоугольный.

∠КАС = ∠А : 2 = 60° : 2 = 30° (АК - биссектриса)

АК - СК = 8 см.

Пусть СК = х см ⇒ АК = (х+8) см

• Катет, лежащий против угла 30°, равен половине гипотенузы.

⇒ АК = 2 СК

х + 8 = 2х

х = 8

СК = 8 см;  АК = 8 + 8 = 16 (см).

3. Рассмотрим ΔАВК.

∠ВАК = 30° (АК - биссектриса)

∠В = 30° (п.1)

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ ΔАВК - равнобедренный.

Значит:

АК = КВ = 16 см.

Отрезок ВК равен 16 см.