Предмет: Геометрия,
автор: lyddy
Помогите решить по геометрии. Касательная к окружности
Приложения:
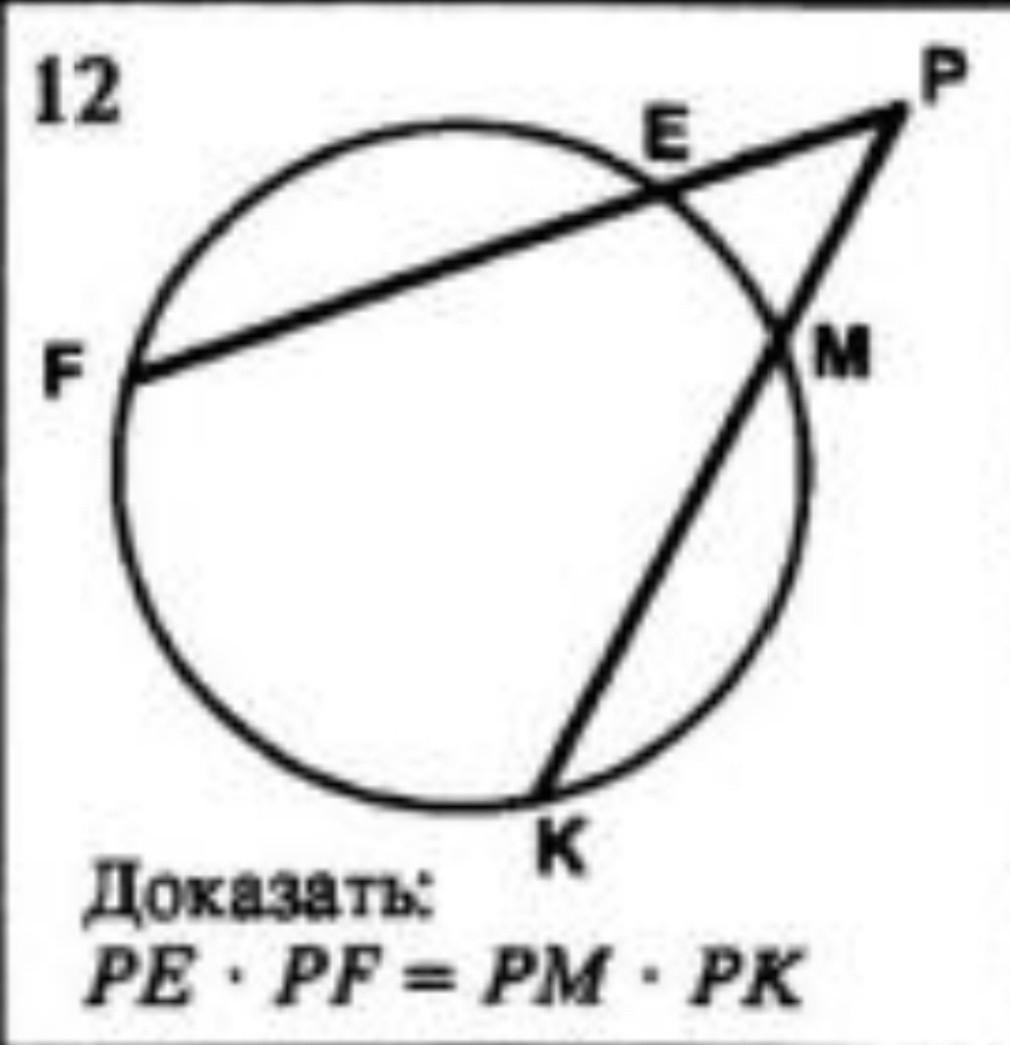
Ответы
Автор ответа:
1
Доказательство:
Лемма. Пустьо из точки , лежащей вне окружности, проведены касательная
и секущая
. Докажем, что
образован касательной
и хордой
, проходящей через точку касания
. Тогда
является вписанным углом, опирающимся на дугу
. Тогда
Получается, что
Рассмотрим треугольники и
.
Они подобны (угол общий,
)
Следовательно, верно равенство
Доказательство
Проведем касательную к окружности из точки
.
Получим, что и
- секущие, а значит по доказанной лемме верны равенства
и
Получаем, что , что и требовалось доказать.
Приложения:
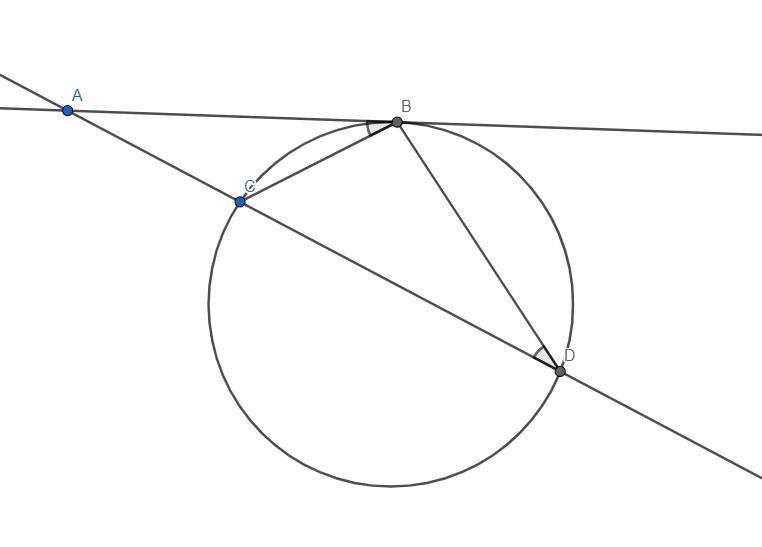
unknownx0:
Не прикрепил рисунок, если можно, отправьте пожалуйста на исправление, прикреплю
Похожие вопросы
Предмет: Русский язык,
автор: вова631
Предмет: Русский язык,
автор: vasilchenkova06
Предмет: Русский язык,
автор: ира12345612
Предмет: Математика,
автор: gssss