Предмет: Алгебра,
автор: anastasiyastepanova0
знайти похідну фукції
Приложения:
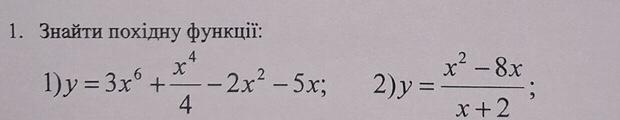
Ответы
Автор ответа:
1
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: adangilov
Предмет: Қазақ тiлi,
автор: клей5
Предмет: Русский язык,
автор: VLAD7001
Предмет: Биология,
автор: Аноним
Предмет: Физика,
автор: evaa210