Question

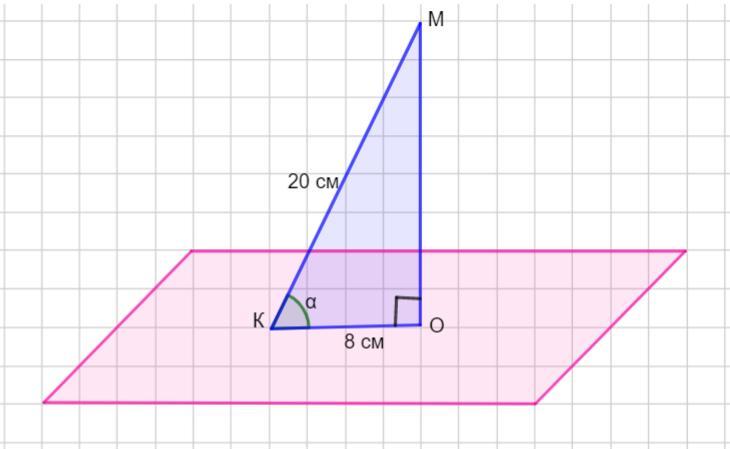
Наклонная МК длиной 20 см имеет проекцию КО равную 8 см.
Найти расстояние от точки М до плоскости и угол между наклонной МК и плоскостью

Answer 1

Ответ:

Расстояние от точки М до плоскости равно 4√21 см, угол между наклонной и плоскостью равен $arccos(0,4)$ или  66°.

Объяснение:

По условию наклонная МК = 20 см, проекция наклонной КО = 8 см.

Найдем расстояние от точки М до плоскости. Длина отрезка МО  - это расстояние от точки М до плоскости.

Рассмотрим Δ МОК - прямоугольный. Найдем катет МО по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$MK^{2} =MO^{2} +OK^{2} ;\\MO^{2}=MK^{2} -OK^{2};\\MO=\sqrt{MK^{2} -OK^{2}};\\MO=\sqrt{20^{2} -8^{2} } =\sqrt{(20-8)(20+8)} =\sqrt{12\cdot28} =\sqrt{4\cdot3\cdot7\cdot4} =4\sqrt{21}$

Значит, расстояние от точки М до плоскости равно 4√21 см.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Найдем косинус угла между наклонной и плоскостью,

то есть ∠ МКО.

$cos\alpha =\dfrac{OK}{KM};\\\\ cos\alpha =\dfrac{8}{20}=\dfrac{4}{10} =0,4$

$\alpha =arccos(0,4)$.

Если воспользоваться таблицами Брадиса, то угол между наклонной и плоскостью примерно равен 66°.

#SPJ1