Предмет: Алгебра,
автор: Braistar1337
8 клас тема Рівняння що зводяться до квадратних
Приложения:
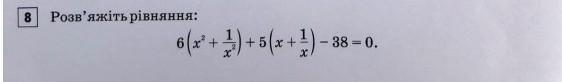
Ответы
Автор ответа:
1
Объяснение:
Пусть:
Ответ: x₁=-3, x₂=-1/3, x₃=1/2, x₄=2.
Похожие вопросы
Предмет: Русский язык,
автор: виктор166
Предмет: Русский язык,
автор: Катя3773
Предмет: Окружающий мир,
автор: khard1996
Предмет: Английский язык,
автор: samurainarkodiller