Question

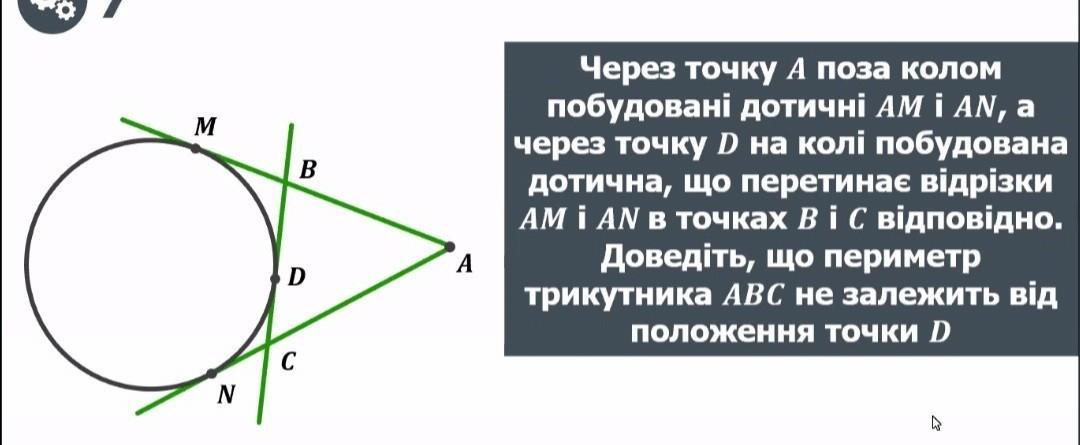
Задача на фото.Даю 100 балов​

Answer 1

Ответ:

Объяснение:

Решение задачи основано на известном факте, что если из точки к окружности проведены две касательные (в нашем случае это касательные AM и AN, BM и BD, CN и CD), то они равны. Отсюда, вне зависимости от положения точки D на меньшей дуге MN, периметр треугольника ABC равен

P=AC+CB+BA=AC+CD+DB+BA=AC+CN+MB+BA=AN+AM=2AN.

Задача решена.