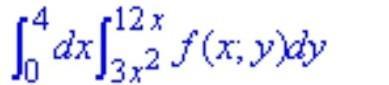Question

Измените порядок интегрирования в двойном интеграле

Answer 1

Ответ:

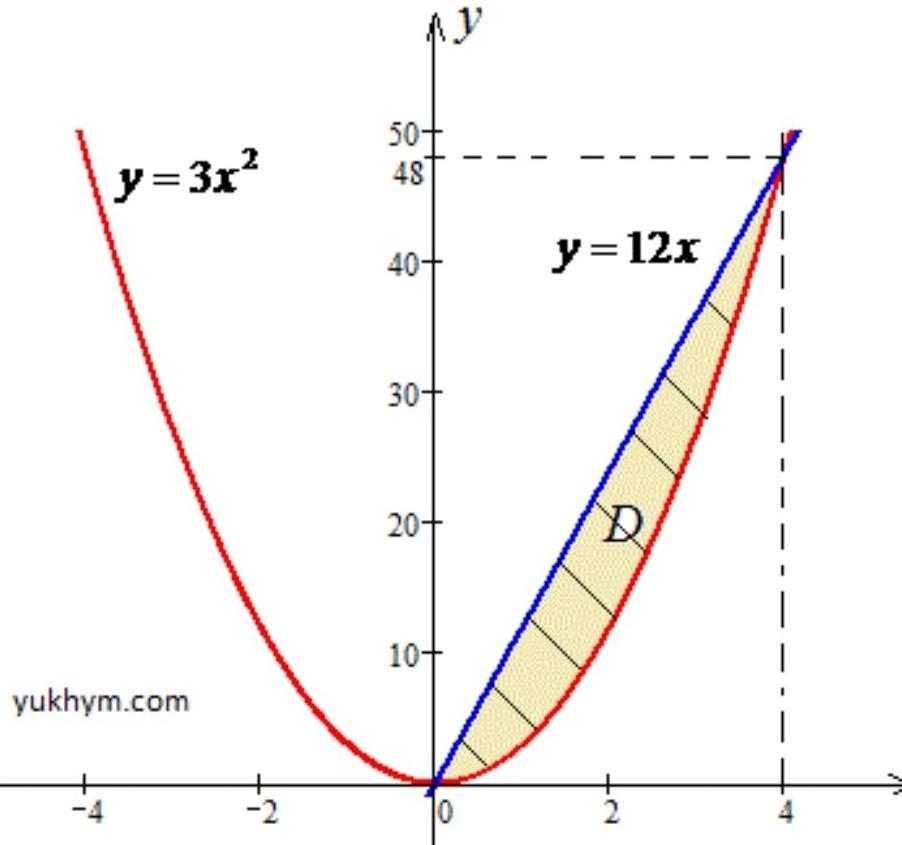
Решение: Построим область интегрирования ограниченую кривыми

0≤x≤4, 3x2≤y≤12x, где

y=3x2 - парабола с вершиной в точке O(0;0) и ветками вверх;

y=12x - прямая, которая проходит через начало координат O(0;0).

График области интегрирования приведен на рисунке.

двойной интеграл

В этом примере "игрек" изменяется от нижней кривой (параболы) к верхней (прямой), в это время "икс" пробегает значение от 0 до 4.

При изменении порядка интегрирования мы будем пробегать значение от первой кривой по "иксу" (прямой) ко второй (параболы), "игрек" в это время будет проходить значение от 0 ко второй точке пересечения заданных кривых.

Отсюда следует, что для изменения порядка интегрирования нужно найти точки пересечения кривых, дальше для изменения пределов нужно перейти от y(x) к x(y) для этих самых пределов.

Выражаем заданные функции y(x) через переменную y:

y=3x2, отсюда (перед корнем взяли знак "+", поскольку x≥0)

y=12x, отсюда x=y/12.

Найдем точки пересечения:

y=3x2=12x, отсюда

Расставим пределы в заданной области:

D: 0≤y≤48

Answer 2

Ответ:

возьмем любой интегралл.

Пошаговое объяснение:

Изменить порядок интегрирования в двойном интеграле:

фото его снизу.

Решение: Построим область интегрирования ограниченую кривыми

0≤x≤4, 3x2≤y≤12x, где

y=3x2 - парабола с вершиной в точке O(0;0) и ветками вверх;

y=12x - прямая, которая проходит через начало координат O(0;0).

График области интегрирования приведен на рисунке. (снизу)