Предмет: Геометрия,
автор: Аноним
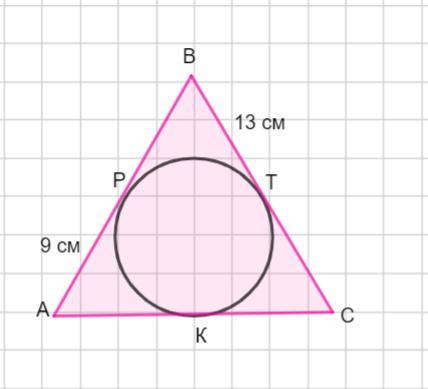
У трикутник ABC вписано коло. Р, Т, К- точки дотику кола до його сторін AB, BC, АС. Знайти довжину відрізка ТС, якщо AP=9 см, ВТ=13 см, а периметр трикутника дорівнює 56 см.
Ответы
Автор ответа:
3
Ответ:
ТС= 6 см
Объяснение:
Пусть в Δ АВС вписана окружность. Точки Р,Т,К - точки касания сторон АВ, ВС, АС соответственно.
По условию АР=9 см, ВТ =13 см, а периметр треугольника равен 56 см.
Отрезки касательных к окружности, проведенных из одной точки, равны.
Тогда
ВТ= ВР = 13 см . Сторона АВ = АР + ВР = 9+13=22 см.
АК = АР = 9 см. Пусть СК =СТ = х см. Тогда сторона
АС = АК +СК = (9 + х ) см, ВС = ВТ +СТ = (13 +х ) см.
Так как периметр равен треугольника равен 56 см, то составляем уравнение:
Если х= 6 см, то СК=СТ =6 cм.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: RamikMOZG
Предмет: Английский язык,
автор: 1Laima123
Предмет: Українська мова,
автор: olyakrakatitsa
Предмет: История,
автор: Фурия24