Question

ПОМОГИТЕ ПОЖАЛУЙСТА, НАДО СРОЧНО!
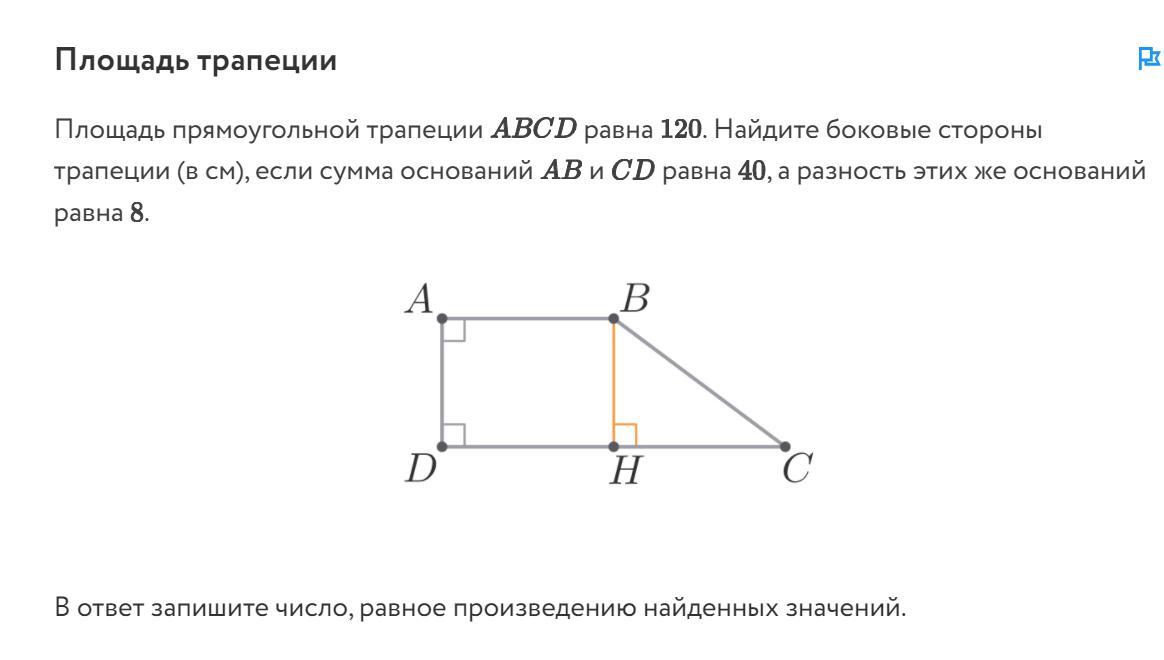
Площадь прямоугольной трапеции ABCD равна 120. Найдите боковые стороны трапеции (в см), если сумма оснований АВ и CD равна 40, а разность этих же оснований
равна 8.
В ответ запишите число, равное произведению найденных значений.

Answer 1

Ответ:

Объяснение:

Площадь трапеции равна полусумме оснований на высоту. Отсюда найдем высоту BH, которая в прямоугольной трапеции равна стороне AD:
BH = AD = S/((AB+DC)/2) = 120/20 = 6.
В прямоугольном треугольнике BHC катет BH = 6, а катет HC равен разности оснований = 8.
Гипотенуза BC по теореме Пифагора:
BC = √(CH²+BH²) = √(8²+6²) = 10