Предмет: Алгебра,
автор: kruzkacaa523
решите систему уравнений методом подстановки
Приложения:
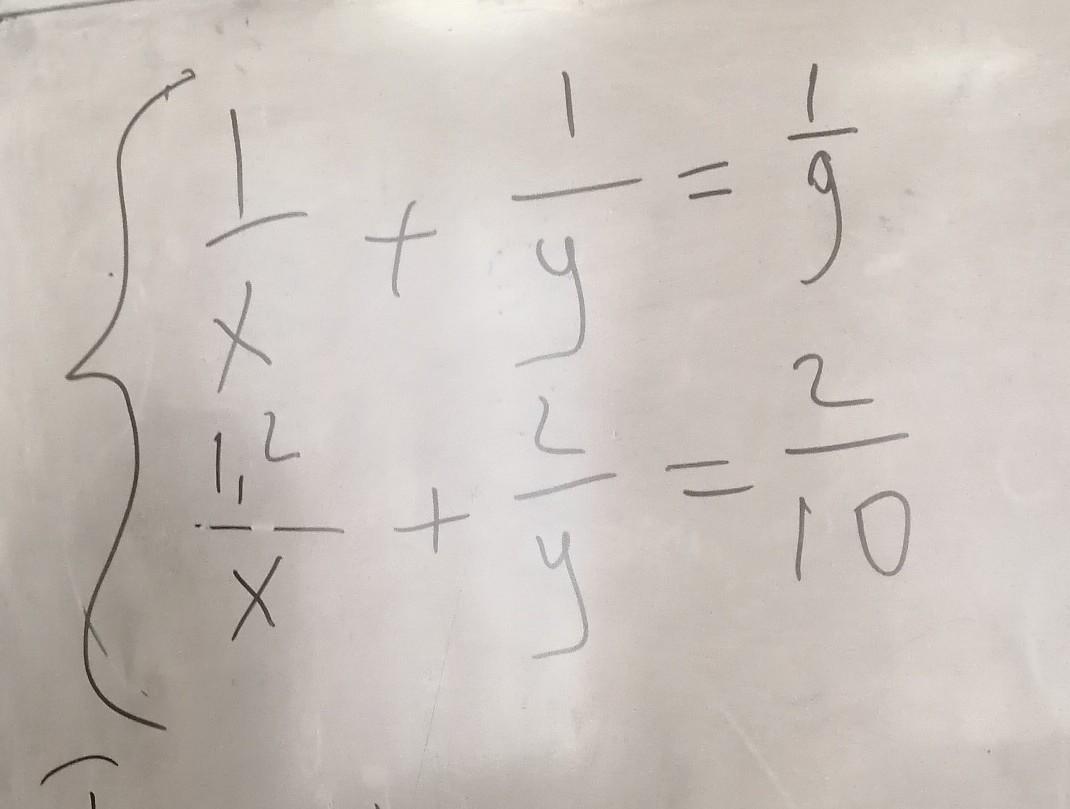
Ответы
Автор ответа:
1
Объяснение:
Пусть:
Вычитаем из первого уравнения второе:
Ответ: (36;12).
Похожие вопросы
Предмет: Русский язык,
автор: влвл2
Предмет: Другие предметы,
автор: isaevkamaldin
Предмет: Английский язык,
автор: Tgmivgjo
Предмет: Математика,
автор: nastenkalivelike
Предмет: Геометрия,
автор: zhidelevairina13