6.101. (2) упростить выражение.
ответ должен быть:
1/a^2 + 1
прошу, помогите, полностью решение с объяснением.
совсем не понимаю эту тему(( (7 класс)
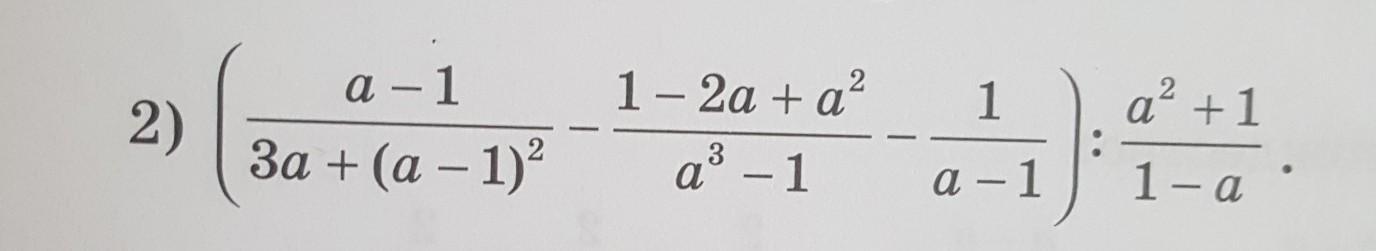
Ответы
Ответ:
В решении.
Объяснение:
1) Преобразовать знаменатель первой дроби:
3а + (а - 1)² =
= 3а + а² - 2а + 1 =
= а² + а + 1;
2) Преобразовать знаменатель второй дроби (разность кубов, разложить по формуле):
а³ - 1 = (а - 1)(а² + а + 1);
Очевидно, что общий знаменатель для трёх дробей в скобках:
(а - 1)(а² + а + 1);
Дополнительные множители:
над числителем первой дроби (а - 1); над числителем второй дроби 1; над числителем третьей дроби (а² + а + 1);
3) Получили дробь:
[((а - 1)(а - 1)) - (1 - 2а + а²) - 1*(а² + а + 1)]/[(а - 1)(а² + а + 1)] =
раскрыть скобки:
= (а² - а - а + 1 - 1 + 2а - а² - а² - а - 1)/[(а - 1)(а² + а + 1)] =
привести подобные в числителе:
= (-а² - а - 1)/[(а - 1)(а² + а + 1)] =
в числителе вынести минус:
= -(а² + а + 1)/[(а - 1)(а² + а + 1)] =
= числитель и знаменатель сократить на (а² + а + 1);
= -1/(а - 1); итог действий в скобках;
4) Деление:
-1/(а - 1) : (а² + 1)/(1 - а) =
преобразовать знаменатель первой дроби:
= -1/-(1 - а) : (а² + 1)/(1 - а) =
= 1/(1 - а) : (а² + 1)/(1 - а) =
= (1 * (1 - а))/((1 - а)(а² + 1)) =
числитель и знаменатель сократить на (1 - а);
= 1/(а² + 1). Итог решения.