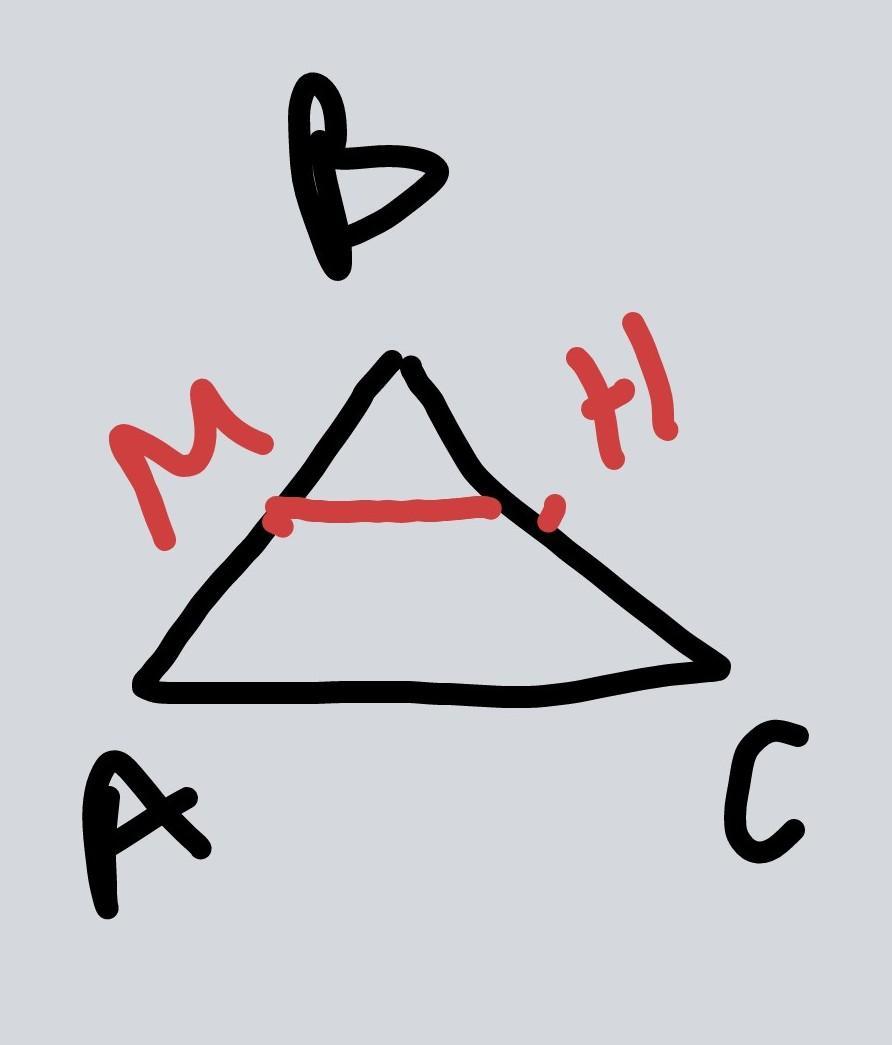
Дан треугольник АВС,в котором ∠А = ∠С = 60°. Докажите, что расстояние от точки В до прямой МН равно расстоянию между прямыми МН и АС, если М и Н - середины сторон АВ и ВС треугольника АВС соответственно.
помогите пожалуйста
Ответы
Объяснение:
Сумма углов в треугольнике =180.
Если два угла у нас по 60,то третий 180-60-60=60 тоже 60,значит треугольник равносторонний.
МН - средняя линия треугольника АВС, так как соединяет середины сторон. Значит МН параллельна АС (по свойству средней линии).
Проведём медиану(она же и высота) в треугольнике АВС ,назовём её ВК. Пусть ВК пересекает МН в точке О. По теореме Фалеса: ВО:ОК=АМ:МВ, что и доказывает то что нужно доказать.
В случае,если вам не известна теорема Фалеса:
Рассмотрим два треугольника : АВС и ВМН. Они оба равносторонние, поэтому подобны. АВ:ВМ=ВС:ВМ. Тогда коэффициент подобия равен 2. Но и все их соответсвующие элементы тоже подобны. Проведём медиану (высоту) в тругольнике АВС из вершины В. Высота треугольника АВС будет в два раза больше высоты труегольника ВМН. Откуда и вытекает то что требовалось доказать.