Question

Прошу помогите пожалуйста Вычислите площадь фигуры (предварительно построив ее)
б)у=2х^2u у=8

Answer 1

Ответ:  $\frac{64}{3}$

Объяснение:

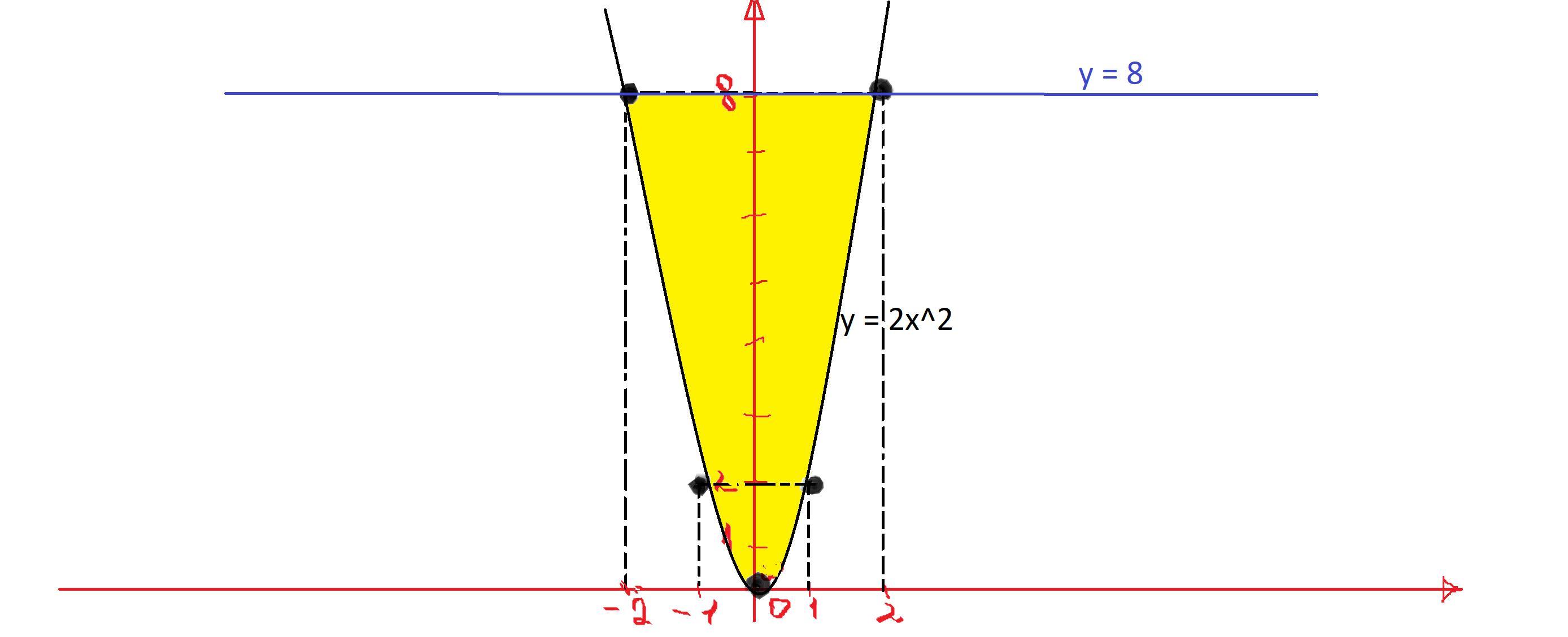
Нарисуем график (желтым закрашена площадь, которую нужно найти).

• y = 8 - это просто прямая, параллельная Ох.
• y = $2x^{2}$ - это классическая парабола, сжатая в 2 раза.
• Они пересекаются в точках (-2, 8) и (2, 8).

Есть правило, что если на отрезке [a, b] какая-то непрерывная функция f(x) больше или равна g(x), то площадь фигуры, ограниченной этими графиками на отрезке [a, b] будет равна $\int\limits^a_b {(f(x) - g(x))} \, dx$

Очевидно, что y = 8 больше или равна y = $2x^{2}$ на отрезке [-2, 2]. Посчитаем соответствующий интеграл:

$\int\limits^2_{-2} {(8-2x^{2}) } \, dx =(8x-2\frac{x^{3} }{3} )|\limits^2_{-2} =32-\frac{32}{3} =\frac{64}{3}$

Это и есть ответ.