Предмет: Геометрия,
автор: Adhshbaaaa
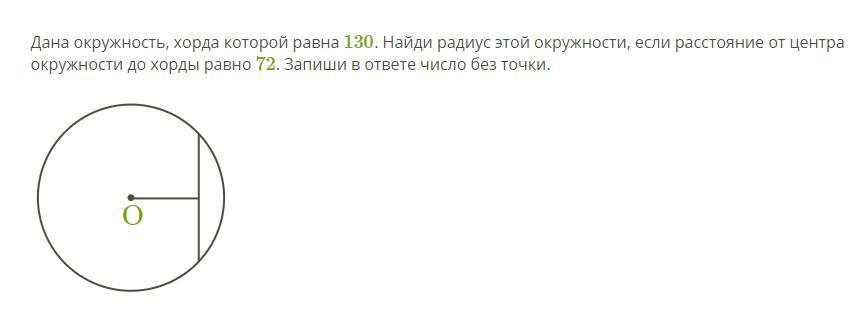
дана окружность хорда которой равна 130
Приложения:
Ответы
Автор ответа:
1
Если мы проведем отрезок, то получим прямоугольный треугольник с катетами 72 и 130/2=65.
По теореме Пифагора:
72^2+65^2=9409.
Вычисляем корень и получается, что гипотенуза равна 97, т.к. гипотенуза в этом треугольнике - радиус окружности, то диаметр, равный 2R, получается 97х2=194.
Ответ:194
По теореме Пифагора:
72^2+65^2=9409.
Вычисляем корень и получается, что гипотенуза равна 97, т.к. гипотенуза в этом треугольнике - радиус окружности, то диаметр, равный 2R, получается 97х2=194.
Ответ:194
fatimkau:
Тут надо найти только радиус
Автор ответа:
1
Можно найти радиус окружности по теореме Пифагора
Отметим точками А В С
Проведём от центра окружности к точке А отрезок и получается прямоугольный треугольник
Сторона АВ равна 65 тк АС равна 130
По теореме Пифагора находим гипотенузу ОА
ОА^2=ОВ^2 + АВ^2
ОА^2= 72^2+65^2
ОА=97
Ответ:97
Отметим точками А В С
Проведём от центра окружности к точке А отрезок и получается прямоугольный треугольник
Сторона АВ равна 65 тк АС равна 130
По теореме Пифагора находим гипотенузу ОА
ОА^2=ОВ^2 + АВ^2
ОА^2= 72^2+65^2
ОА=97
Ответ:97
Похожие вопросы
Предмет: Английский язык,
автор: nat1674
Предмет: Русский язык,
автор: Дратути24324254664
Предмет: Окружающий мир,
автор: Аноним
Предмет: Математика,
автор: artchannel126
Предмет: Физика,
автор: andreymdobrovol