Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
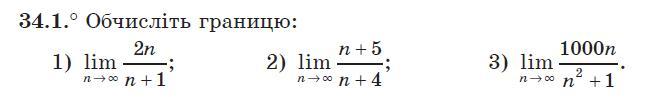
Ответы
Автор ответа:
2
Ответ:
Пределы:
1)
2)
3)
Примечание:
Теоремы: (при условии, что - сходящиеся последовательности)
Предел суммы:
Предел произведения:
Следствие из предела произведения:
, где
Предел частного:
при условии, что
.
Объяснение:
34.1
1)
2)
3)
.
Похожие вопросы
Предмет: Русский язык,
автор: klonelex
Предмет: Английский язык,
автор: Vitali750
Предмет: Українська мова,
автор: galag9955
Предмет: Биология,
автор: milenagoncarova
Предмет: Биология,
автор: nikitosikkudin050