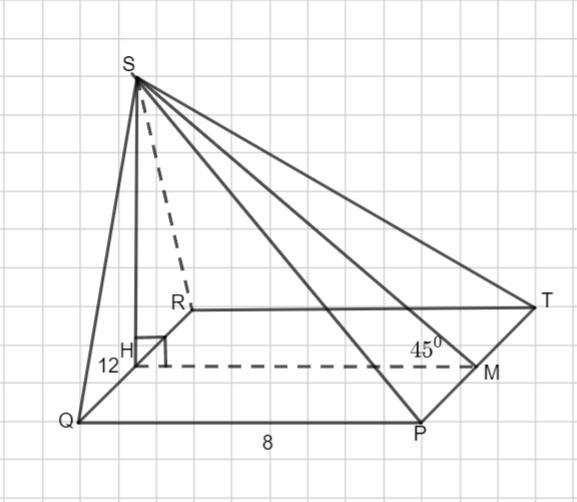
В основании пирамиды SPQRT лежит прямоугольник PQRT. Высота пирамиды проходит через середину ребра QR. QR=12, QP=8. Боковая грань, противолежащая ребру QR, наклонена к плоскости основания под углом 45°. Найди площадь полной поверхности пирамиды.
Ответы
Ответ:
Площадь полной поверхности пирамиды равна (224+48√2) кв. ед
Объяснение:
По условию задана пирамида SPQRT.
Основание PQRT - прямоугольник.
QR=12 ед., QР=8 ед.
Н- середина QR, SН - высота пирамиды. ∠ SMH =45°.
Найдем площадь полной поверхности заданной пирамиды.
Площадь полной поверхности равна сумме площадей 5 граней.
Найдем площадь основания, то есть площадь прямоугольника. Для этого надо длину умножить на ширину.
кв. ед.
Рассмотрим Δ SHM - прямоугольный , так как SH - высота.
Если ∠ SMH =45°, то ∠HSM =90°- 45°=45° ( сумма острых углов прямоугольного треугольника равна 90°).
Если в треугольнике два угла равны , то треугольник равнобедренный.
Δ SHM -равнобедренный
SH= HM= QP= 8 ед.
Найдем гипотенузу SM по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
ед.
Найдем площадь грани SQR , площадь треугольника, как полупроизведение стороны на высоту, проведенную к основанию.
Найдем площадь грани SPT
Рассмотрим ΔQHS - прямоугольный.
QH= 12:2=6 ед., так как точка H - середина QR
Найдем SQ по теореме Пифагора
ед.
Так как по условию PQRT - прямоугольник, то RQ⊥ QP .
По теореме о трех перпендикулярах SQ⊥ QP и треугольник ΔSQP - прямоугольный.
Площадь прямоугольного треугольника равна полупроизведению катетов.
Площадь Δ SRT равна площади ΔSQP и равна 40 кв. ед.
Найдем площадь полной поверхности пирамиды
S= 96+ 48+48√2 +40+40 =144+80+48√2=224+48√2 кв. ед.
Площадь полной поверхности пирамиды равна (224+48√2) кв. ед.
#SPJ1