Question

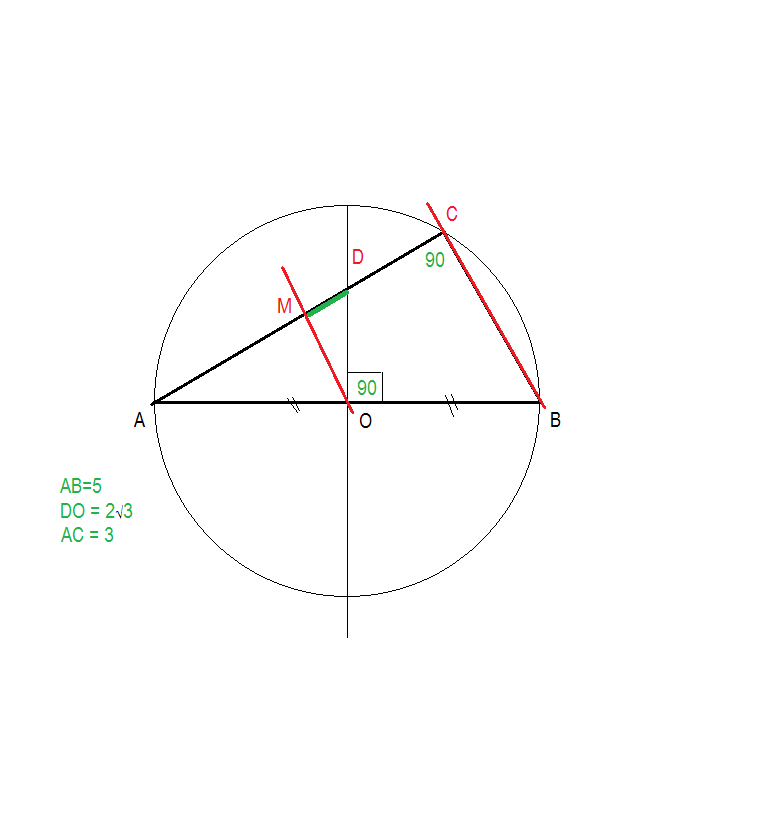
Дано: АВС, угол ACB =90°,

О – центр описанной окружности,

АМ = МC, OD перпендикуляр (ABC), АВ = 5,

АС = 3, DO = 2$sqrt{3}$

Найдите: MD

 

 

Answer 1

делаем рисунок по условию
угол
ACB =90°, значит треуг АВС  - прямоугольный
АВ = 5, АС = 3
BC^2 = AB^2 - AC^2 = 5^2 - 3^2 = 16
BC = 4
АМ = МC
АO = OB
значит ОМ - средняя линия треуг АВС 
OM = BC/2 =4/2 =2
OM || BC 
т.к. ACB =90° , значит OMD =90°
треуг OMD  - прямоугольный
DO = 2√3
MD^2 = DO^2 - OM^2 = (2√3)^2 - 2^2 = 12 - 4 =8
Найдите: MD  = √8 = 2√2

ответ MD  = 2√2