Question

помогите пожалуйста(

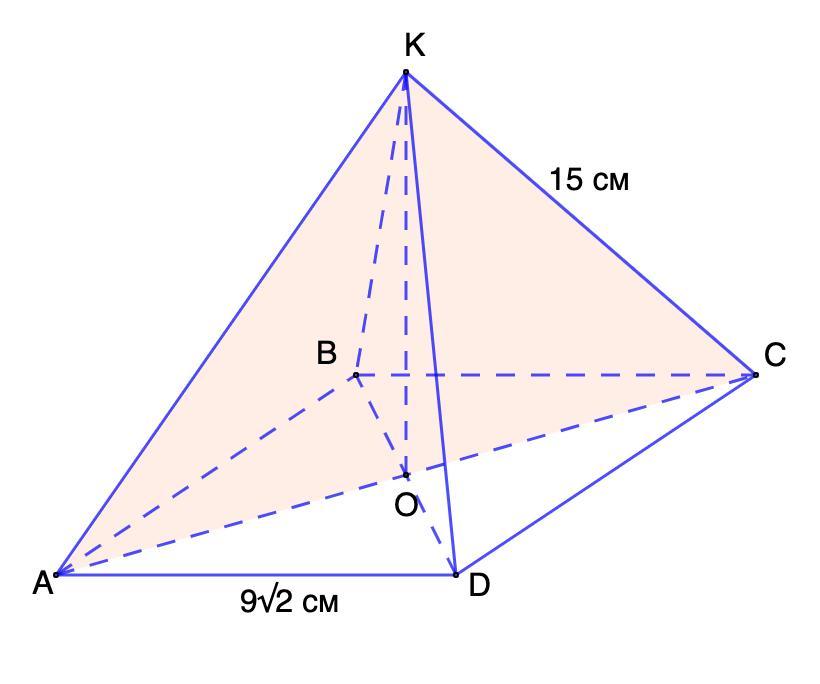
1. сторона основания правильной четырёхугольной пирамиды равна 9 корень 2 см, а боковое ребро 15 см. Найдите площадь диагонального сечения пирамиды.

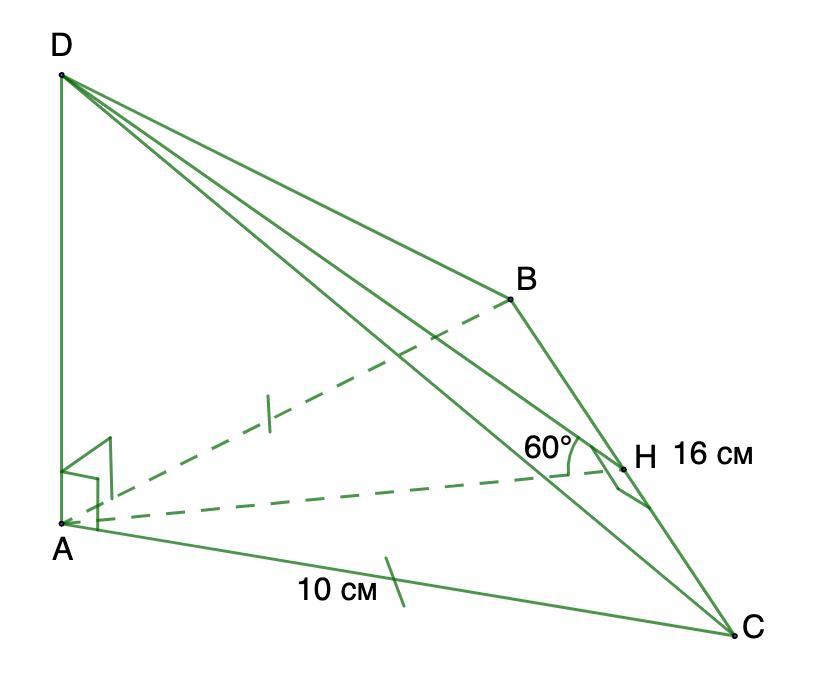
2. основанием пирамиды DABC является равнобедренный треугольник ABC, в котором AB=AC и равно 10 см, ВС=16. боковые грани DAC и DAB пирамиды перпендикулярны к плоскости основания, а грань DBC наклонена к ней под углом 60 градусов. Найдите:
а) высоту пирамиды
б) площадь боковой поверхности пирамиды

Answer 1

Ответ:

1. Площадь диагонального сечения пирамиды равна 108 см².

2. а) Высота пирамиды равна 6√3 см.

б) Площадь боковой поверхности пирамиды равна (60√3 + 96) см².

Объяснение:

1. Найти площадь диагонального сечения пирамиды.

2. Найти:

а) высоту пирамиды

б) площадь боковой поверхности пирамиды

1. Дано: KABCD - правильная пирамида;

AD = 9√2 см; КС = 15 см.

Найти: S(АКС).

Решение:

• В основании правильной четырехугольной пирамиды лежит квадрат.

Рассмотрим ΔАСD - прямоугольный.

По теореме Пифагора найдем АС:

АС² = AD² + BD² = 81 · 2 + 81 · 2 = 324

AC = √324 = 18 (см)

• Диагонали квадрата точкой пересечения делятся пополам.

⇒ ОС = 18 : 2 = 9 (см)

Рассмотрим ΔКОС - прямоугольный.

По теореме Пифагора найдем ОК:

ОК² = КС² - ОС² = 225 - 81 = 144

ОК = √144 = 12 (см)

Рассмотрим ΔАКС.

• Площадь треугольника равна половине произведения высоты на сторону, к которой проведена эта высота.

$\displaystyle S=\frac{1}{2}ah$ , где а - сторона, h - высота.

S(AKC) = 0,5 · AC · KO = 0,5 · 18 · 12 = 108 (см²)

Площадь диагонального сечения пирамиды равна 108 см².

2. Дано: DABC - пирамида.

ΔАВС  - равнобедренный, основание;

АВ = АС = 10 см; ВС = 16 см.

DAC и DAB перпендикулярны АВС.

DBC наклонена к АВС под углом 60 градусов.

Найти: AD; S бок.

Решение:

а)

Рассмотрим ΔАВС - равнобедренный.

АН - высота.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ СН = НВ = 16 : 2 = 8 (см)

Рассмотрим ΔАНС - прямоугольный.

По теореме Пифагора найдем АН:

АН² = АС² - НС = 100 - 64 = 36

АН = √36 = 6 (см)

Рассмотрим ΔADH - прямоугольный.

• Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

⇒  ∠DHA = 60°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ADH = 90° - ∠DHA = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ DH = 2 · AH = 12 см.

По теореме Пифагора найдем AD:

AD² = DH² - AH² = 144 - 36 = 108

AD = √108 = 6√3 (см)

Высота пирамиды равна 6√3 см.

б)

Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней.

Рассмотрим ΔADC и ΔADB - прямоугольные.

DA - общая.

• Если проекции наклонных, проведенных из одной точки, равны, то равны и сами наклонные.

⇒ DC = DB

ΔADC = ΔADB (по катету и гипотенузе)

• Площадь прямоугольного треугольника равна половине произведения катетов.

S(ADC) = S(ADB) = 0,5 · AC · AD = 0,5 · 10 · 6√3 = 30√3 (см²)

Рассмотрим ΔCDB - равнобедренный.

S(CDB) = 0,5 · CB · DH = 0,5 · 16 · 12 = 96 (см²)

Площадь боковой поверхности пирамиды равна:

S бок. = S(ADC) + S(ADB) + S(CDB) = 30√3 + 30√3 + 96 = (60√3 + 96) (см²)

Площадь боковой поверхности пирамиды равна (60√3 + 96) см².

#SPJ1