Question

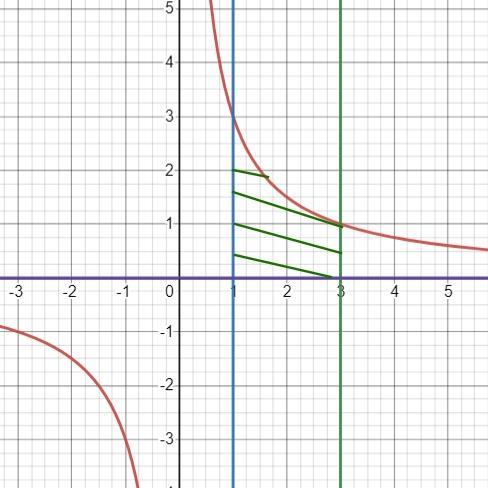
Обчислити площу фігури, обмеженою лініями у = 3/x, y = 0, х = 1, х = 3​

Answer 1

Ответ:

площадь фигуры S ≈ 3,5928

Пошаговое объяснение:

Площадь считаем по формуле Ньютона-Лейбница

$\displaystyle S=\int\limits^a_b {\bigg (y_1(x) -y_2(x)\bigg)} \, dx$

Рисуем графики.

По графикам определяем

1. фигуру;
2. пределы интегрирования: b = 1;  a = 3;
3. функции у₁(х) и у₂(х): за функцию у₁(х) берут  функцию, график которой лежит "выше" на координатной плоскости. У нас получается у₁(х) = 3/х; у₂(х) = 0

Считаем интеграл

$\displaystyle S= \int\limits^3_1 {\frac{3}{x} } \, dx =3ln(x)\bigg |_1^3=3ln(3)-3ln(1)=ln(27)\approx 3,2958$