Предмет: Алгебра,
автор: Supergirl455
Помогите пожалуйста !
Приложения:
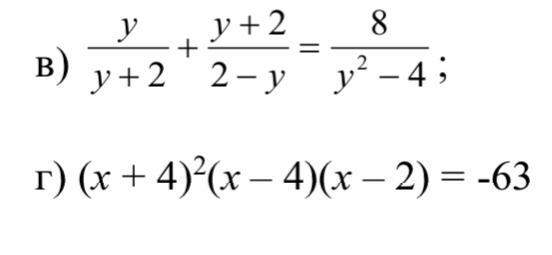
Ответы
Автор ответа:
4
Ответ:
в) нет решений; г) нет решений
Объяснение:
в) Обычно в такой задаче советуют приводить к общему знаменателю, но мы пойдем другим путем, выделив слева целые части и разложив правую часть, воспользовавшись очень полезной формулой
Имеем:
Решений нет.
г) Замена x-3=t; получаем уравнение
Ясно, что левая часть принимает отрицательные значения только на интервале (-1;1), поэтому можно ограничиться только этими значениями. Приводим уравнение к виду
Если решений нет.
Если решений нет.
Похожие вопросы
Предмет: Английский язык,
автор: Luntic19
Предмет: Английский язык,
автор: Akbotta
Предмет: Русский язык,
автор: mishahakimov26
Предмет: Химия,
автор: olegbavoliak
Предмет: Русский язык,
автор: chengis