Решить задачу линейного программирования графическим способом.

Ответы
Ответ:
fmax = –1
Пошаговое объяснение:
Введем на плоскости прямоугольную систему координат Ox₁x₂ (это позволит применить алгоритм графического метода).
Начнем с нахождения значения переменных x₁ и x₂, при которых целевая функция принимает максимальное значение. Действовать будем пошагово в соответствии с алгоритмом решения ЗЛП графическим методом.
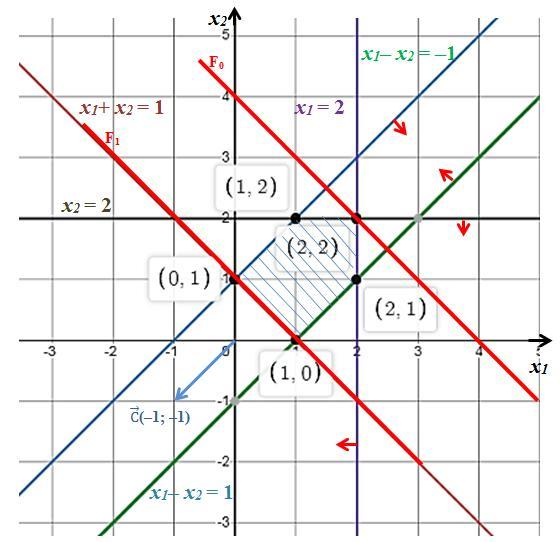
Шаг 1. Для того чтобы найти множество точек, координаты которых удовлетворяют первым 5 неравенствам системы ограничений, нужно построить граничные прямые.
x₁ + x₂ = 1
x₁ – x₂ = –1
x₁ – x₂ = 1
x₁ = 2
x₂ = 2
Затем определить соответствующие полуплоскости. Для этого определим, по какую сторону от прямой располагается точка O(0; 0). Красные стрелки показывают нужные полуплоскости.
Множества точек, координаты которых удовлетворяют всем 5 неравенствам, изображены на рисунке (заштрихованный пятиугольник).
Шаг 2. Строим вектор (–1; –1).
Шаг 3. Линия уровня F₀ задается уравнением –x₁–x₂ = const. На рисунке построена линия уровня, соответствующая –x₁–x₂ = –4.
Шаг 4. Сначала найдем значения переменных x₁, x₂, при которых целевая функция принимает максимальное значение. Поэтому перемещаем F₀ по направлению вектора до линии уровня, являющейся границей полуплоскости, целиком содержащей область допустимых решений (заштрихованный пятиугольник).
Такой линией является прямая F₁, проходящая через точки (0; 1) и (1; 0). Следовательно,
максимального значения линейная целевая функция достигает в точках (0; 1) и (1; 0) (так как линейная функция принимает свои наибольшие значения на границах отрезка!).
Шаг 5. Таким образом, целевая функция имеет максимальное значение в точке (1; 0) (или (0; 1)): fmax = –1–0 = –1.