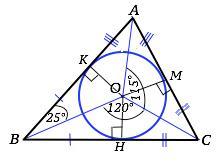
2. Рис. 747. AB, BC, AC - касательные, уголBOC = 120°, уголABO = 25°, уголAOC = 115°. Найти углы треугольника АОВ. Доказать: O- точка пересечения биссектрис треугольника АВС.
Ответы
Решение ( подробно).
АВ, ВС и АС - составляют треугольник. Все стороны треугольника АВС касаются окружности, ⇒ треугольник описан около этой окружности, а окружность - вписана в него.
Градусная мера круга равна 360º,⇒
в ∆ АОВ ∠АОВ=360°- (∠ВОС+∠АОС)=125°
Из суммы углов треугольника ∠ОАВ=180°-(125°+25°)=30°
Обозначим К - точку касания стороны АВ, М - стороны АС и Н - стороны ВС. Радиусы, проведенные в точку касания, перпендикулярны касательной.
Рассмотрим ∆ ВОК и ∆ ВОН. Оба прямоугольные, имеют общую гипотенузу и по равному катету (ОК=ОН - радиусы). Если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны ⇒ ∆ ВОК=∆ ВОН, углы КВО=НВО, т.е. ВО - биссектриса угла В. Аналогично доказывается, что СО и АО - биссектрисы углов С и А треугольника АВС. Следовательно, O- точка пересечения биссектрис треугольника АВС. Доказано.
======================
Итак, Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.