Предмет: Геометрия,
автор: pri740063
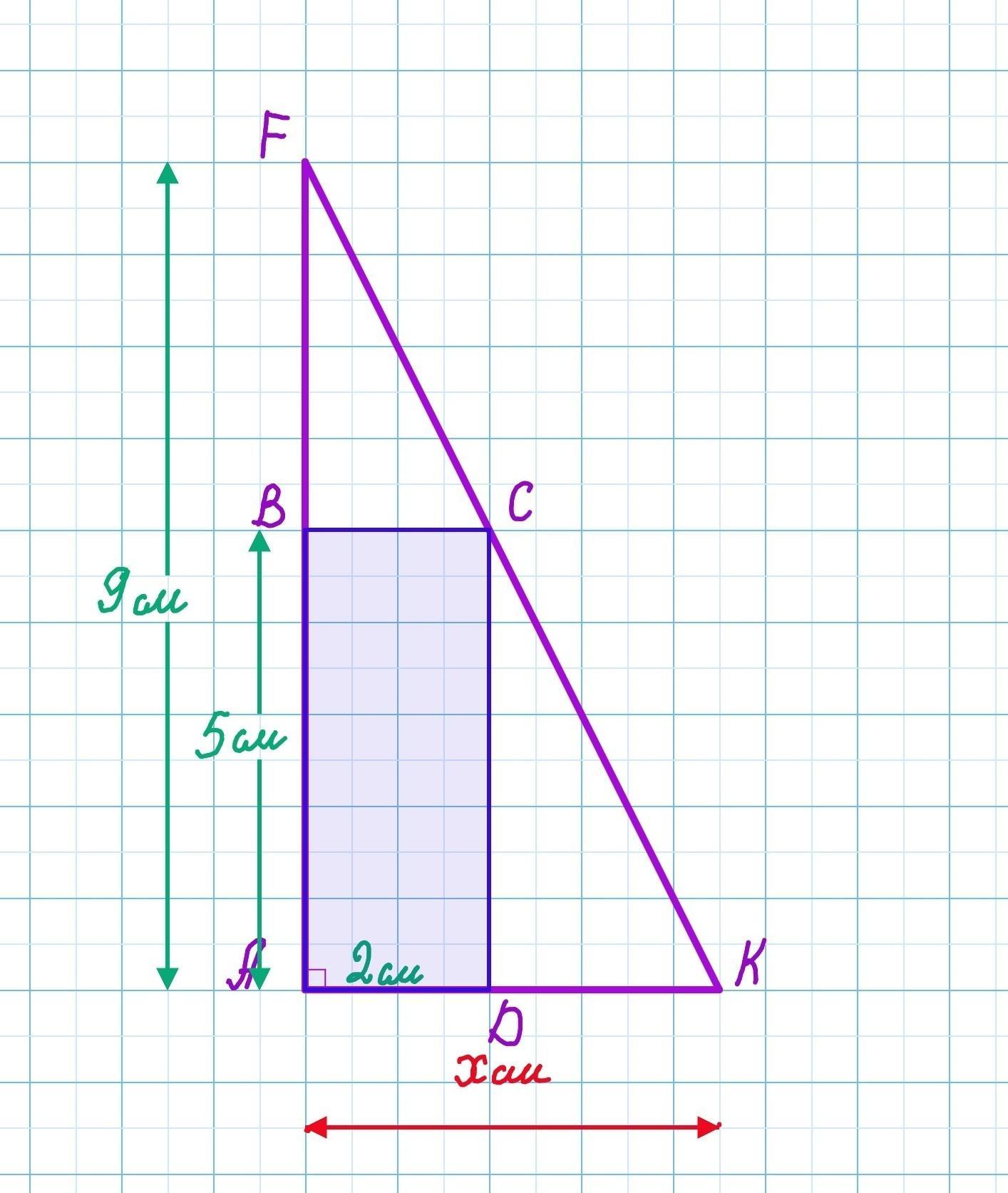
Задание 4 (20 баллов). Прямоугольник ABCD вписан в треугольник AFK c прямым углом А. Стороны прямоугольника АВ и AD лежат на катетах AF и АК соответственно. Найдите АК, если AD = 2 см, АВ = 5 см, AF = 9 см.
Ответы
Автор ответа:
11
Прямоугольник ABCD вписан в треугольник AFK c прямым углом А. Стороны прямоугольника АВ и AD лежат на катетах AF и АК соответственно. Найдите АК, если AD = 2 см, АВ = 5 см, AF = 9 см.
Ответ:
AK=4,5 см.
Объяснение:
Так как АBCD - прямоугольник, то ∠FBC=∠CDK=90°.
BC II AD, следовательно ∠BCF=∠DKC как соответственные углы при пересечении параллельных прямых BC и AD секущей FK.
△FBC подобен △FAK по двум углам ( 1 признак подобия).
Из подобия треугольников следует пропорциональность соответственных сторон:
FB=FA-AB=9-5=4 см
BC=AD=2 см, как противолежащие стороны прямоугольника.
см
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: катя3800
Предмет: Қазақ тiлi,
автор: гоша128
Предмет: Русский язык,
автор: Robertino06
Предмет: История,
автор: olesyauglova06
Предмет: Химия,
автор: vasenina199033