Question

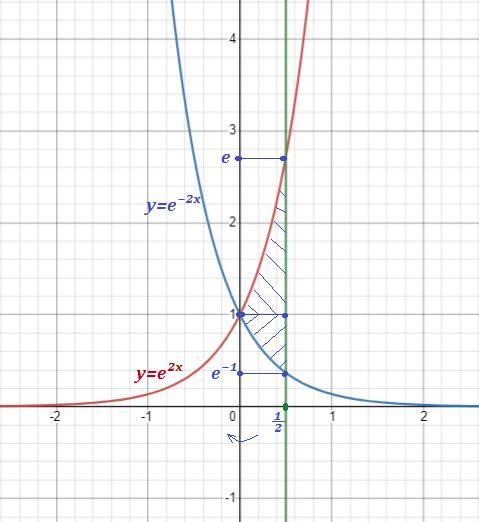
Обчислити об'єм тіла,утвореного обертанням навколо осі Оy фігури,обмеженої лініями $y=e^{2x}, y= e^{-2x}, x=\frac{1}{2}$

Answer 1

Решение.

$\bf y=e^{2x}\ ,\ y=e^{-2x}\ ,\ x=\dfrac{1}{2}$  

Точки пересечения графиков:  1)  $\bf y=e^{2x}$  и  $\bf x=\dfrac{1}{2}$   в точке  $\bf \Big(\dfrac{1}{2}\ ;\ e\, \Big)$  ,

2)   $\bf y=e^{-2x}$  и  $\bf x=\dfrac{1}{2}$   в точке  $\bf \Big(\dfrac{1}{2}\ ;\ e^{-1}\, \Big)$  .  

Объём тела, полученного вращением заданной фигуры вокруг оси

ОУ, вычисляем ,применив формулу

 $\bf \displaystyle V_{oy}=\pi \int\limits^{a}_{b}\, x^2(y)\, dy$

Выразим переменные х из обеих функций .

$\bf y=e^{2x}\ \ \Rightarrow \ \ 2x=lny\ ,\ x=\dfrac{1}{2}\, lny\\\\y=e^{-2x}\ \ \Rightarrow \ \ -2x=lny\ ,\ x=-\dfrac{1}{2}\, lny$

$\displaystyle \bf V_{oy}=\pi \int\limits_{e^{-1}}^1\, \Big(\frac{1}{4}-\frac{1}{4}\, ln^2y\Big)dy+\pi \int\limits^{e}_1\, \Big(\frac{1}{4}-\frac{1}{4}\, ln^2y\Big)dy$  

Вычислим отдельно интеграл.

$\displaystyle \bf \int ln^2x\, dx=\Big[u=ln^2x\ ,\ du=\frac{2\, lnx\, dx}{x}\ ,\ dv=dx\ ,\ v=x\ \Big]=\\\\\\=x\cdot ln^2x-2\int lnx\, dx=\Big[\ u=lnx\ , \ du=\frac{dx}{x}\ ,\ dv=dx\ ,\ v=x\ \Big]=\\\\\\=x\cdot ln^2x-2\cdot \Big(x\cdot lnx-\int \, dx\Big)=x\cdot ln^2x-2x\cdot lnx+2x+C\ ;$

$\displaystyle \bf V_{oy}=\Big(\frac{\pi}{4}\, y-\frac{\pi}{4}\, (y\cdot ln^2y-2y\cdot lny+2y)\Big)\Big|_{e^{-1}}^1+\\\\\\+\Big(\frac{\pi}{4}\, y-\frac{\pi}{4}\, (y\cdot ln^2y-2y\cdot lny+2y)\Big)\Big|^{e}_1=\\\\\\=\frac{\pi}{4}-\frac{\pi}{4}\Big(1\cdot 0-0+2\Big)-\frac{\pi}{4}\, e^{-1}+\frac{\pi}{4}\, \Big(e^{-1}+2e^{-1}+2e^{-1}\Big)+\\\\\\+\frac{\pi}{4}\, e-\frac{\pi}{4}\Big(e-2e+2e)-\frac{\pi}{4}+\frac{\pi}{4}\Big(0-0+2\Big)=$

$\displaystyle \bf =\frac{\pi}{4}-\frac{\pi}{2}+\frac{\pi}{4}\cdot 4e^{-1}-\frac{\pi}{4}+\frac{\pi }{2}=\pi \, e^{-1}=\frac{\pi}{e}$