Question

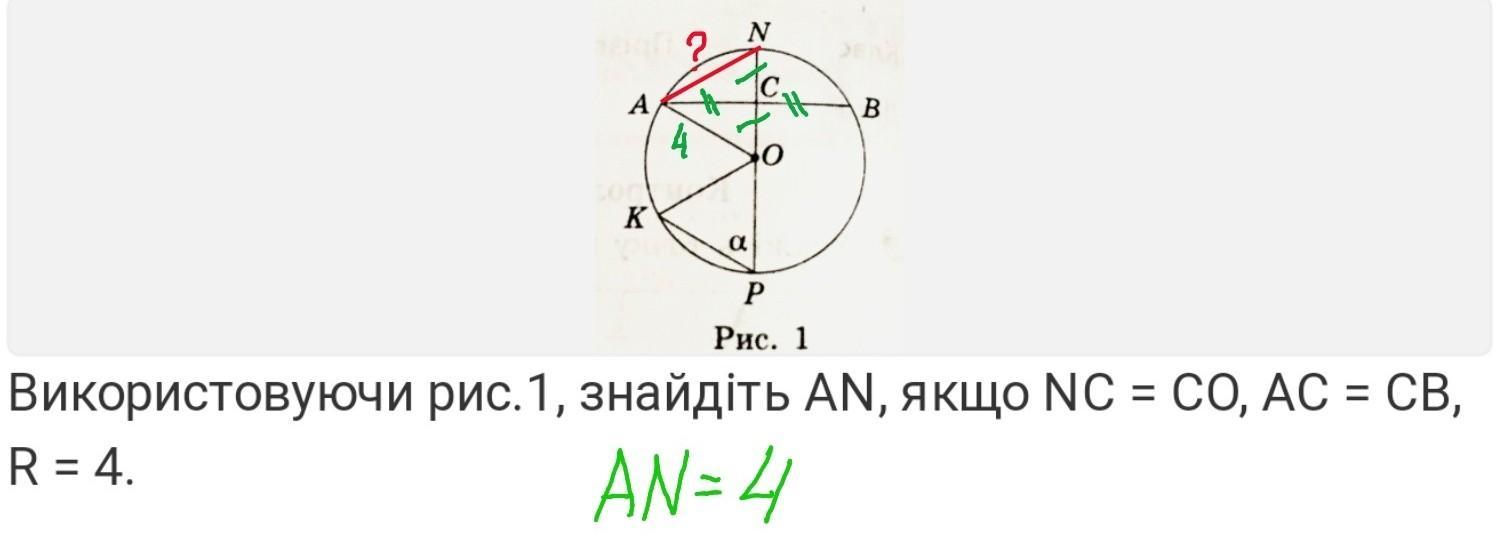
знайдіть AN якщо NC=CO, AC=CB, R=4

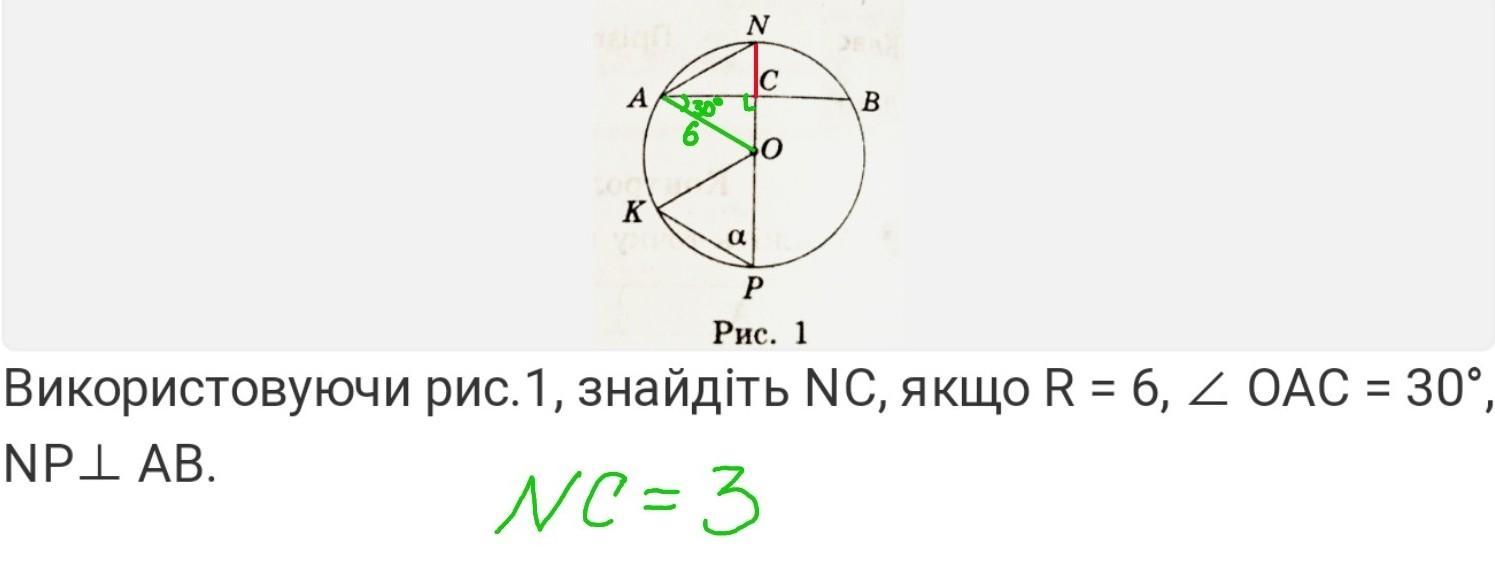
знайдіть NC якщо R=6, кут AOC=30, NP|AB
a. 3см
б. 4см
в. 5см
г. 2см
д. 6см​

Answer 1

Ответ:

а) AN=4 ед

б) NC=3 ед

Объяснение:

• Хорда - це відрізок, який з'єднує дві точки заданої кривої.
• Якщо діаметр ділить хорду, яка не є діаметром, навпіл, то цей діаметр перпендикулярний цій хорді.
• Вірно і зворотне - якщо діаметр перпендикулярний хорді, то цей діаметр ділить цю хорду навпіл.

а) знайдіть AN якщо NC=CO, AC=CB, R=4

NP - діаметр кола з центром в точці О. АВ - хорда.

AC=CB => діаметр NP ділить хорду АВ навпіл. Тому AB⟂NP.

В △OAN висота АС є також медіаною, так як NC=CO за умовою.

Отже △OAN - рівнобедрений.

В рівнобедреному трикутнику бічні сторони рівні => AN=AO=4 ед.

б) знайдіть NC якщо R=6, кут AOC=30, NP⟂AB

Діаметр NP перпендикулярний хорді АВ, отже △АОС - прямокутний.

Катет СО лежить навпроти кута 30°, тому він дорівнює половині гіпотенузи АО:

СО=½• АО=½•6=3

NC= NO-CO=R-CO=6-3=3 ед

_______

#SPJ1