Предмет: Алгебра,
автор: valeriailo201217
Помогите решить, пожалуйста!!! Алгебра 10 класс
Приложения:
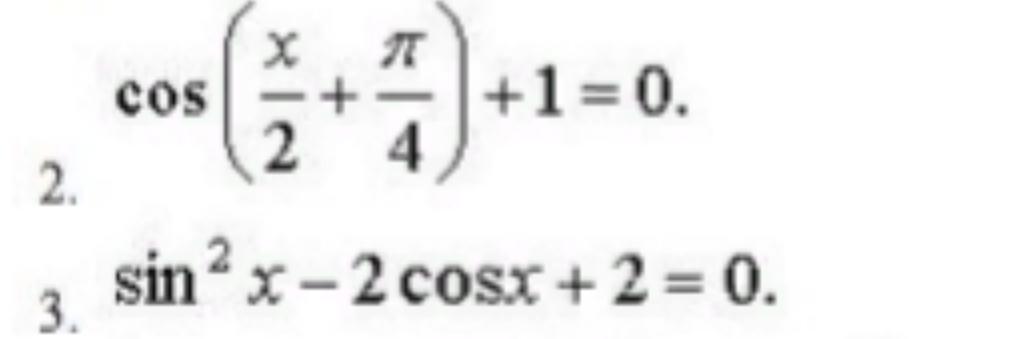
Ответы
Автор ответа:
2
valeriailo201217:
большое спасибо!!!
Пожалуйста
Автор ответа:
6
Решить уравнения 1) cos(x/2 + π/4)+1=0; 2) sin^2 x - 2cosx+2=0.
Ответ:
Формулы:
Если cos x = b и |b|≤1, то
Объяснение:
С формулы выразим cos^2 x и подставим вместо sin^2 x:
Введём замену cos^2 x = u
Возвращаемся к замене:
большое спасибо!!!
Похожие вопросы
Предмет: Английский язык,
автор: 11092005
Предмет: Английский язык,
автор: AlexFresh18
Предмет: Английский язык,
автор: annaanet
Предмет: Математика,
автор: andreimasalski
Предмет: Қазақ тiлi,
автор: AssemFun