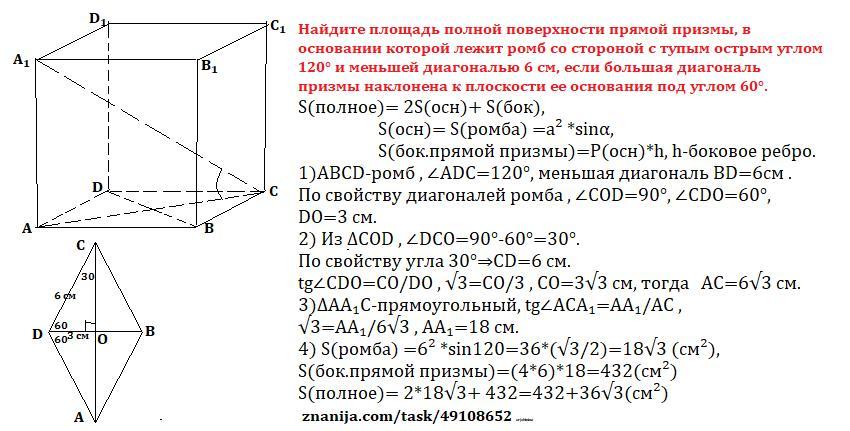
Найдите площадь полной поверхности прямой призмы, в основании которой лежит
ромб со стороной с тупым острым углом 120° и меньшей диагональю 6 см, если большая диагональ призмы наклонена к плоскости ее основания под углом 60°.
можно с подробным решением пожалуйста
Ответы
Найдите площадь полной поверхности прямой призмы, в основании которой лежит ромб со стороной с тупым острым углом 120° и меньшей диагональю 6 см, если большая диагональ призмы наклонена к плоскости ее основания под углом 60°.
Объяснение:
S(полное)= 2S(осн)+ S(бок),
S(осн)= S(ромба) =а² *sinα,
S(бок.прямой призмы)=Р(осн)*h, h-боковое ребро.
1)АВСD-ромб , ∠ADC=120°, меньшая диагональ BD=6см .По свойству диагоналей ромба , ∠COD=90°, ∠CDO=60°, DO=3 см.
2) Из ΔСОD , ∠DCO=90°-60°=30°. По свойству угла 30°⇒CD=6 см.
tg∠CDO=CO/DO , √3=CO/3 , CO=3√3 см, тогда АС=6√3 см.
3)ΔАА₁С-прямоугольный, tg∠АСА₁=АА₁/АС , √3=АА₁/6√3 , АА₁=18 см.
4) S(ромба) =6² *sin120=36*(√3/2)=18√3 (см²),
S(бок.прямой призмы)=(4*6)*18=432(см²).
S(полное)= 2*18√3+ 432=432+36√3(см²)