Предмет: Геометрия,
автор: IslaSique1973
1.В треугольнике ABC известно, что АВ = 16, ВС = 10, since =¾. найдите площадь треугольника АВС.
2. через точку А, лежащую вне окружности, проведены дае прямые. одна прямая касается окружности в точке К. другая прямая пересекает окружность в точках В и С, причем АВ = 9, ВС = 27. найдите АК.
Ответы
Автор ответа:
3
Ответ:
1) 60 см^2; 2) 18 см
Объяснение:
1) Даны две стороны треугольника ABC: AB = 16 см, BC = 10 см.
Дальше, очевидно, опечатка: не since = 3/4, а sin B = 3/4.
Найти площадь треугольника.
Решение:
Есть формула для площади треугольника через две стороны и угол между ними:
S(ABC) = 1/2*AB*BC*sin B = 1/2*16*10*3/4 = 10*3*16/8 = 60 см^2
2) Дана окружность и 2 прямые: касательная и секущая из точки A.
Касательная касается окружности в точке K.
Секущая пересекает окружность в точках B и C, причем расстояния:
AB = 9 см, BC = 27 см.
Найти длину отрезка AK.
Смотрите рисунок.
Есть свойство касательной и секущей, выходящих из одной точки:
AK^2 = AB*AC
В нашем случае: AB = 9см, AC = AB + BC = 9 + 27 = 36 см.
AK^2 = 9*36 = 324
AK = √324 = 18 см.
Приложения:
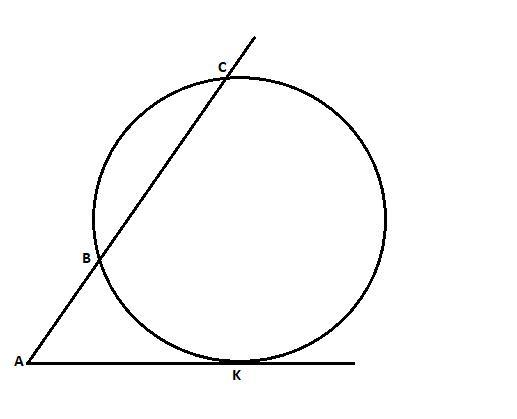
Похожие вопросы
Предмет: Немецкий язык,
автор: russhax
Предмет: Русский язык,
автор: LLIERLOCK
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: angola7725
Предмет: Музыка,
автор: elovka1