Предмет: Математика,
автор: hwason2003
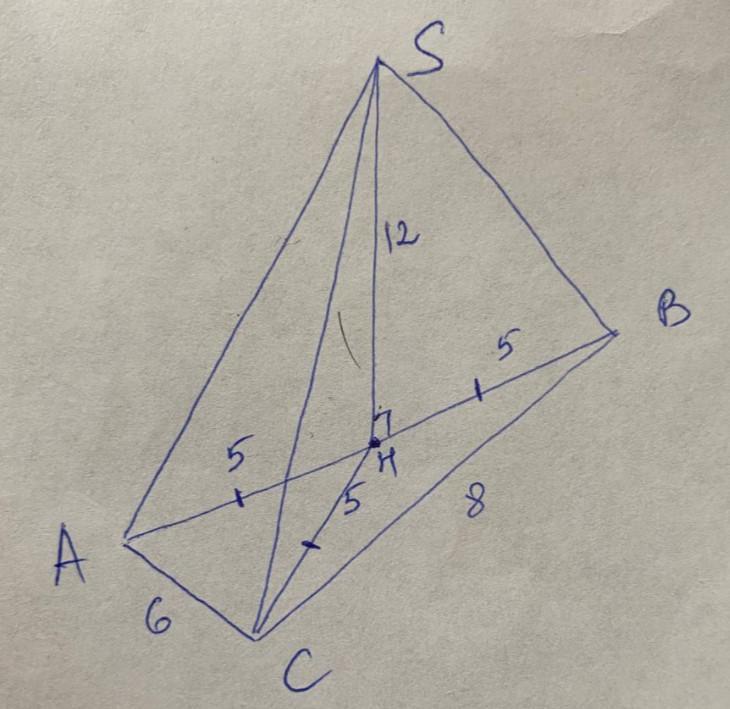
В основании пирамиды SABC лежит прямоугольный треугольник ABC с катетами 6 и 8, высота пирамиды, проходящей через середину гипотенузы AB, равна 12.
Найди боковые ребра пирамиды
Ответы
Автор ответа:
1
Ответ:
SA = SC = SB = 13.
Пошаговое объяснение:
По теореме Пифагора сразу найдем гипотенузу треугольника в основании: АВ = 10.
Пусть Н - середина гипотенузы.
АН = ВН = СН = 5 (медиана, проведенная к гипотенузе, равна половине гипотенузы).
Рассмотрим треугольник SCH - он прямоугольный (т.к. SH - высота пирамиды, т.е. SH перпендикулярно плоскости основания АВС, а значит и любой прямой в плоскости АВС).
По теореме Пифагора:
SC^2 = SH^2 + CH^2
SC^2 = 12^2 + 5^2 = 144 +25 = 169 = 13^2
Значит, SC = 13
При этом SA = SB = SC (т.к. SH - перпендикуляр, SA, SB, SC - наклонные, HA, HB, HC - проекции. Равным проекциям соответствуют равные наклонные).
Получили, что SA = SC = SB = 13.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: madina1909
Предмет: Беларуская мова,
автор: даша2678
Предмет: Русский язык,
автор: nikitax523
Предмет: Математика,
автор: rghfgjk
Предмет: Алгебра,
автор: dj666jb