Question

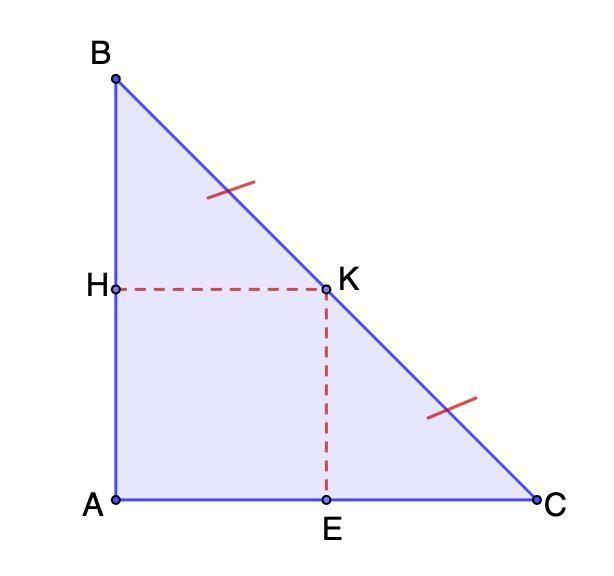
У рівнобедреному прямокутному трикутнику, площа якого 32 см², через середину гіпотенузи провели відрізки, паралельні катетам. Доведіть, що утворений чотирикутник – квадрат та знайдіть його площу.​

Answer 1

Ответ:

Площадь квадрата АНКЕ равна 16 см².

Объяснение:

В равнобедренном прямоугольном треугольнике, площадь которого 32 см², через середину гипотенузы провели отрезки, параллельные катетам. Докажите, что образованный четырехугольник - квадрат и найдите его площадь.​

Дано: ΔАВС - равнобедренный прямоугольный треугольник.

ВК = КС;

КЕ || АВ; КН || АС.

S(ABC) = 32 см².

Доказать: АНКЕ - квадрат,

Найти: S(АНКЕ).

Доказательство:

1. КЕ || АВ; КН || АС;

АВ ⊥ АС;

• Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.

⇒ КЕ ⊥ АС; КН ⊥ АВ.

• Четырехугольник, у которого все углы прямые, называется прямоугольником.

⇒ АНКЕ - прямоугольник.

2. Рассмотрим АВС - равнобедренный, прямоугольный.

⇒ АВ = АС

ВК = КС (условие)

КЕ || АВ (условие)

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ КЕ - средняя линия.

КН || АС

⇒ КН - средняя линия.

• Средняя линия равна половине длины стороны, которую она не пересекает.

⇒ $\displaystyle KE = \frac{1}{2}AB;\;\;\;\;\;KH=\frac{1}{2}AC}$

Так как АВ = АС, то КЕ = КН.

• Противоположные стороны прямоугольника равны.

⇒ КЕ = КН = АН = АЕ.

• Прямоугольник, у которого все стороны равны, называется квадратом.

⇒ АНКЕ - квадрат.

Решение:

3. Найдем катеты ΔАВС.

• Площадь прямоугольного треугольника равна половине произведения катетов.

Пусть АВ = АС = а см

$\displaystyle S(ABC)=\frac{1}{2}a^2\\\\32=\frac{1}{2}a^2\\ \\a^2=64\\\\a=8\;_{(CM)}$

⇒ КЕ = КН = АН = АЕ = 8 : 2 = 4 (см)

• Площадь квадрата равна квадрату его стороны.

S (АНКЕ) = 4² = 16 (см²)

Площадь квадрата АНКЕ равна 16 см².