Question

Менша основа трапеції дорівнює 12 см точка перетину діагоналей віддалена від основ на 4 см і 5 см.Знайдіть площу трапеції ​

Answer 1

Менша основа трапеції дорівнює 12 см точка перетину діагоналей віддалена від основ на 4 см і 5 см.Знайдіть площу трапеції

Ответ:

Площа трапеції дорівнює 121,5 см².

Объяснение:

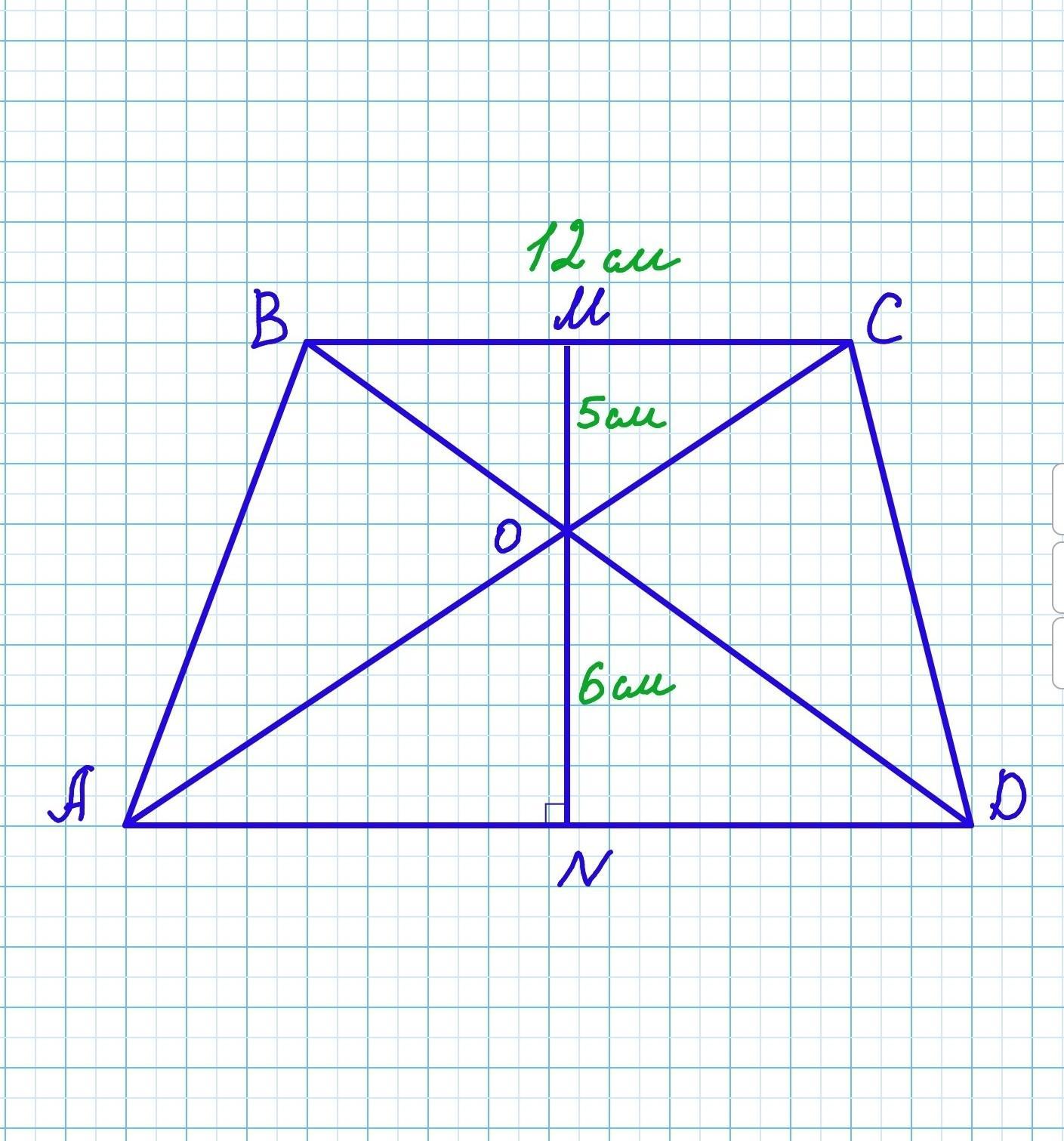
Дано: АВСD - трапеція. AD II BC, BC=12см, MO та ON - відстані від точки О (перетину діагоналей трапеції) до основ трапеції BC і AD, тобто MO⟂BC, ON⟂AD. MO=4 см, ON=5см

Знайти: $S_{ABCD}$.

Розглянемо △COB і △AOD.

∠BCO=∠DAO - як внутрішні різносторонні кути при перетині сичною AC паралельних прямих BC і AD. ∠BOC=∠AOD - як вертикальні.

△COB подібний △AOD за двома кутами. (перша ознака).

У подібних трикутниках відповідні сторони і висоти пропорційні:

$\frac{BC}{AD} = \frac{MO}{ON} \\ \\ \frac{12}{AD} = \frac{4}{5} \\ \\ AD = \frac{12 \times 5}{4} = 15$см

Більша основа AD=15см

Оскільки MO⟂BC, ON⟂AD, то MN⟂AD, MN - висота трапеції ABCD.

MN=MO+ON=4+5=9 см

Площу трапеції знайдемо по формулі:

$S_{ABCD} = \frac{BC + AD}{2} \times MN = \frac{12 + 15}{2} \times 9 = 121,5$см²

#SPJ1