Question

Допоможіть чим можете дуже прошу

Answer 1

Ответ:

ответы в пошаговом объяснении

Пошаговое объяснение:

1.

$\displaystyle \bigg (\frac{u}{v} \bigg)'=\frac{u'v-uv'}{v^2}$

$\displaystyle \bigg(\frac{x^2+2}{3x+2} \bigg)'=\frac{(x^2+2)'(3x+2)-(x^2+2)(3x+2)'}{(3x+2)^2} =\\\\\\=\frac{2x(3x+2)-3(x^2+2)}{(3x+2)^2} =\frac{6x^2+4x-3x^2-6}{(3x+2)^2} =\frac{3x^2+4x-6}{(3x+2)^2}$

$\displaystyle \bigg(\frac{x^2+2}{3x+2} \bigg)'_{x_0=-2}=\frac{3(-2)^2+4*(-2)-6}{(3*(-2)+2)^2}=\frac{12-8-6}{(-4)^2} =-\frac{2}{16} =-0,125$

2.

$\displaystyle \int\limits^4_1 {(10-6x)} \, dx =10 \int\limits^4_1 {} \, dx -6 \int\limits^4_1 {x} \, dx=10x \bigg|_1^4-6\frac{x^2}{2} \bigg|_1^4=30 -45=-15$

$\displaystyle \int\limits^{2\pi}_0 {cos(x*4)} \, dx =\left[\begin{array}{ccc}u=x/4\hfill&du=dx/4\hfill\\o_0=0/4=0&u_1=(2\pi)/4=\pi/2&\\\end{array}\right] =\\\\\\=4\int\limits^{\pi/2}_0 {cos(u)} \, du =4sin(u)\bigg |^{\pi/2}_0=4sin(\pi/2)-4sin(0)=4$

3.

Прежде всего найдем производную. Она понадобится в обоих случаях.

f'(x)=(-x³ + 6x² - 9x - 4)' = -3x² + 12x - 9

а) экстремумы

-3x² + 12x - 9 = 0

D = b² -4ac = 36;    

x₁ = 1;   x₂ = 3;  - это критические точки

f(1) = -8

f(3) = -4

Посмотрим вторую производную.

f''(x) = 12-6x

Теперь знаки производной в критических точках

f''(1) = 6>0 - значит точка x₁ = 1 точка минимума функции.

f''(3) = -6<0 - значит точка x₂ = 3 точка максимума функции.

b) монотонность

Смотрим знаки первой производной на интервалах

(-∞ ;1]

f'(0) = -4   <  0      функция убывает

[1; 3]

f'(2) = 30  > 0      функция возрастает

[3; +∞)

f'(4) = -8   < 0      функция убывает

4.

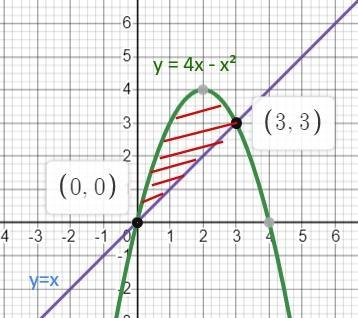
Прежде всего строим графики функций y = 4x - x²   и у = х

Из чертежа получаем фигуру и пределы интегрирования.

Дальше ищем площадь по формуле Ньютона - Лейбница.

$\displaystyle S=\int\limits^a_b {(y_1(x)-y_2(x))} \, dx$

За у₁ (х)   принимаем функцию, график которой находится "выше" на координатной плоскости

у₁(х) = 4х - x²  

у₂(х) = х

пределы интегрирования а = 3; b = 0

Поехали

$\displaystyle S=\int\limits^3_0 {(4x-x^2-x)} \, dx =\int\limits^3_0 {(3x-x^2)} \, dx =3\frac{x^2}{2} \bigg|_0^3-\frac{x^3}{3} \bigg|_0^3=\frac{27}{2} -9=\frac{9}{2}$