Question

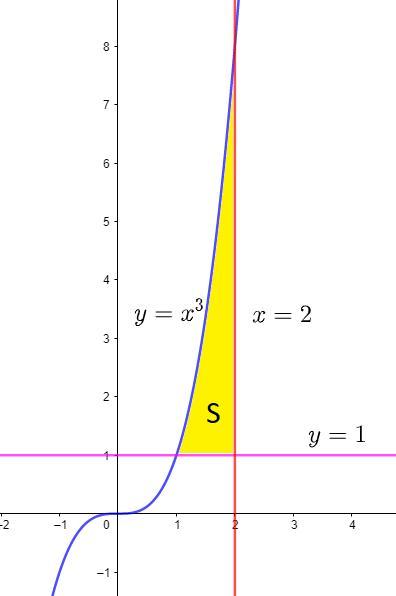
знайдіть площу фігури, обмеженої лініями y=x^3 y=1 x=2

Answer 1

Ответ:

Площадь фигуры равна 2,75 квадратных единиц

Пошаговое объяснение:

По условию фигура ограниченна линиями:

$y = x^{3}$, $y = 1$, $x = 2$

Найдем границы интегрирования:

(для этого необходимо найти точку пересечения графиков

$y = x^{3}$ и $y = 1$

-------------------------

$x^{3} = 1$

$\sqrt[3]{x^{3}} = \sqrt[3]{1}$

$x = 1$

То есть границы интегрирования от 1 до 2.

Так как график $y = x^{3}$ расположен над графиком $y = 1$ на отрезке от 1 до 2, то по формуле Ньютона-Лейбница:

$\displaystyle S = \int\limits^2_1 {(x^{3} - 1)} \, dx = \bigg( \dfrac{x^{4}}{4} - x \bigg) \bigg|_1^2 = \bigg(\dfrac{2^{4}}{4} - 2 \bigg) - \bigg(\dfrac{1^{4}}{4} - 1 \bigg) =2- (-0,75) = 2,75$

квадратных единиц.