Предмет: Геометрия,
автор: WOWWOW123
помогите пожалуйста! даю 50 баллов.
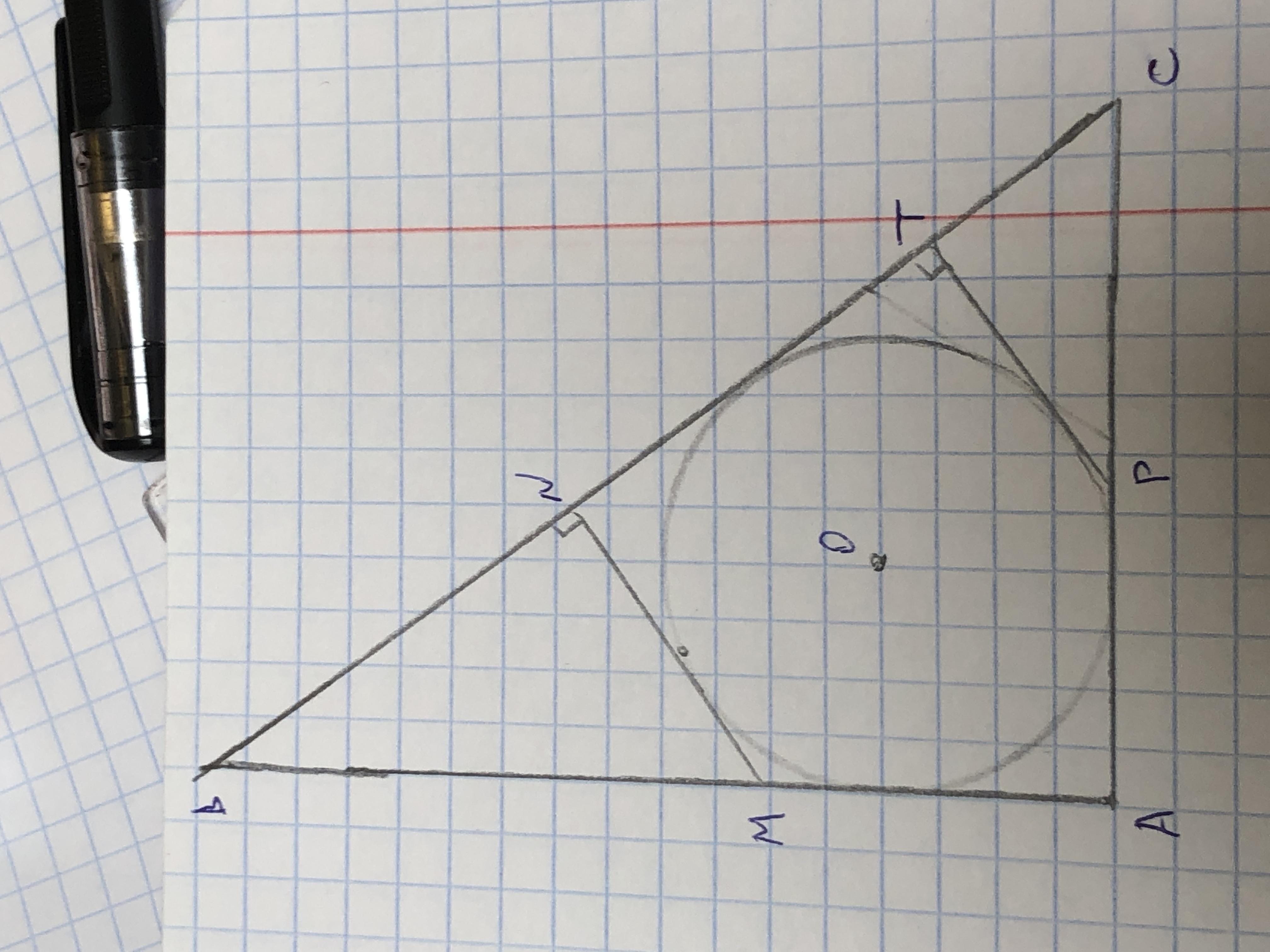
в прямоугольный треугольник вписана окружность. к этой окружности проведены две касательные, являющиеся высотами треугольника к гипотенузе. найдите площадь отделенного пятиугольника AMNTP, если меньший катет - 3, больший катет - 4, гипотенуза - 5
Приложения:
Ответы
Автор ответа:
1
Ответ: 23/6
Объяснение:
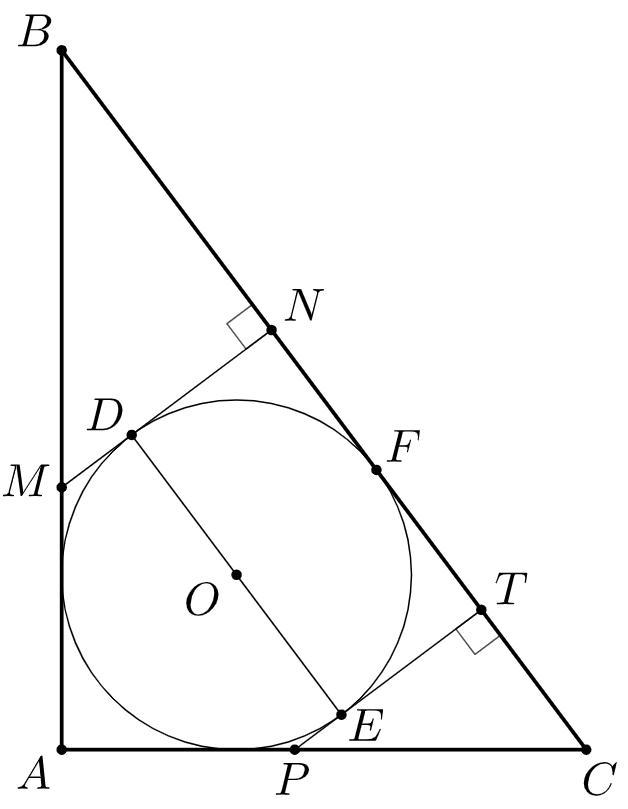
Пусть - точки касания окружности с отрезками
соответственно
по свойству касательных, следовательно
- прямоугольник,
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: новичок244
Предмет: Русский язык,
автор: Ksushsa2007
Предмет: Українська література,
автор: Аноним
Предмет: Химия,
автор: DeepDope
Предмет: Математика,
автор: 77726811190347832