Question

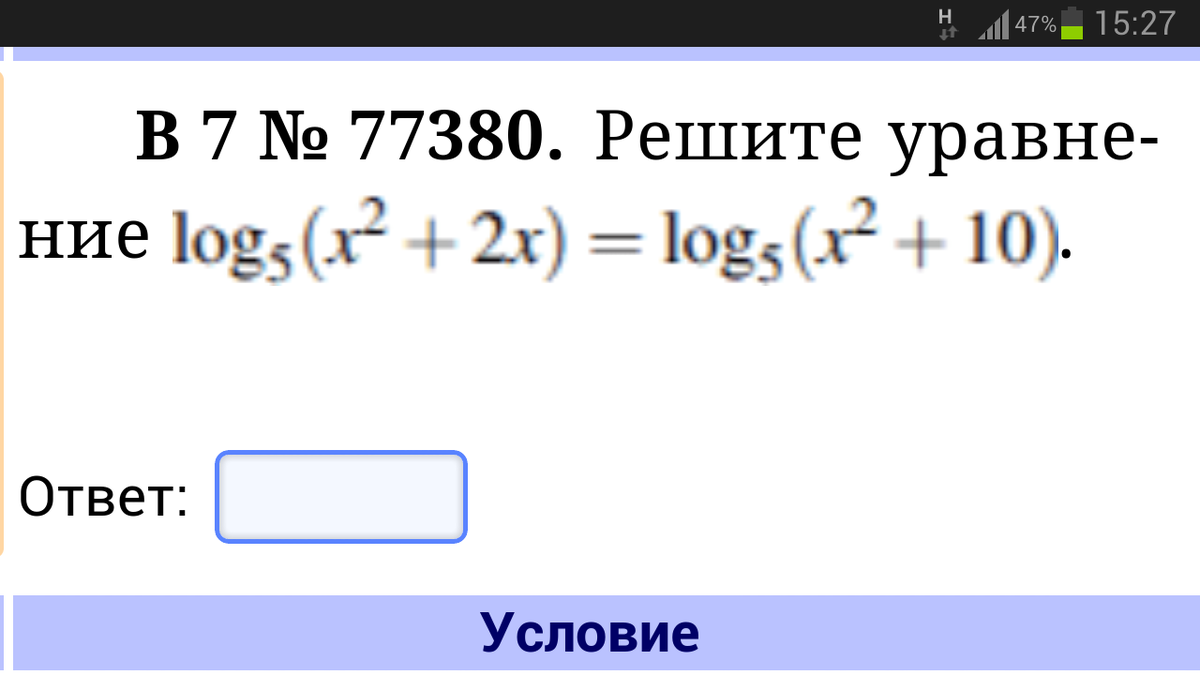
Решите уравнение:
log5 (x^2 + 2x)= log5 (x^2 + 10)

Answer 1

Приравниваем выражения под логарифмом
x^2+2x = x^2 +10
x = 5

проверкой убеждаемся что под логарифмом получается положительное число и найденный корень не постронний

Answer 2

log5 (x^2 + 2x)= log5 (x^2 + 10)
ОДЗ x^2+2x=x(x+2)>0
x<-2 x>0
x^+10>0 всегда квадрат плюс положительное число
x^2+2x=x^2+10
2x=10
x=5