Предмет: Математика,
автор: darkmond169
Найти площадь фигуры , ограниченной заданными линиями
y=x^2+4, y=2x+4-x^2
Ответы
Автор ответа:
0
Ответ:
площадь искомой фигуры S = 1/3
Пошаговое объяснение:
Чтобы найти фигуру, нарисуем чертеж
Получим фигуру и границы интегрирования.
Площадь вычисляем по формуле Ньютона Лейбница
Границы интегрирования b = 0; a = 1
За у₁(х) принимают функцию, график которой лежит "выше" на координатной плоскости.
В нашем случае
у₁(х) = -х² +2х + 4
у₂(х) = х² +4
Посчитаем подынтегральную
у₁(х) - у₂(х) = -х² +2х + 4 -х² -4 = -2х² +2х
Теперь считаем площадь
Приложения:
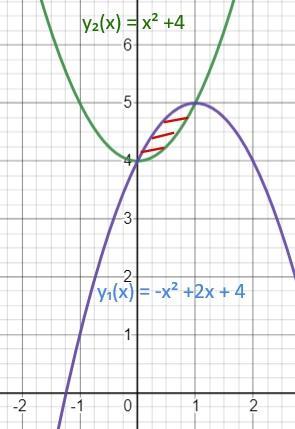
Похожие вопросы
Предмет: Русский язык,
автор: 101061
Предмет: Українська мова,
автор: juggle79
Предмет: Английский язык,
автор: NekitFe
Предмет: Математика,
автор: kitten98655
Предмет: Английский язык,
автор: MichaSverd