Question

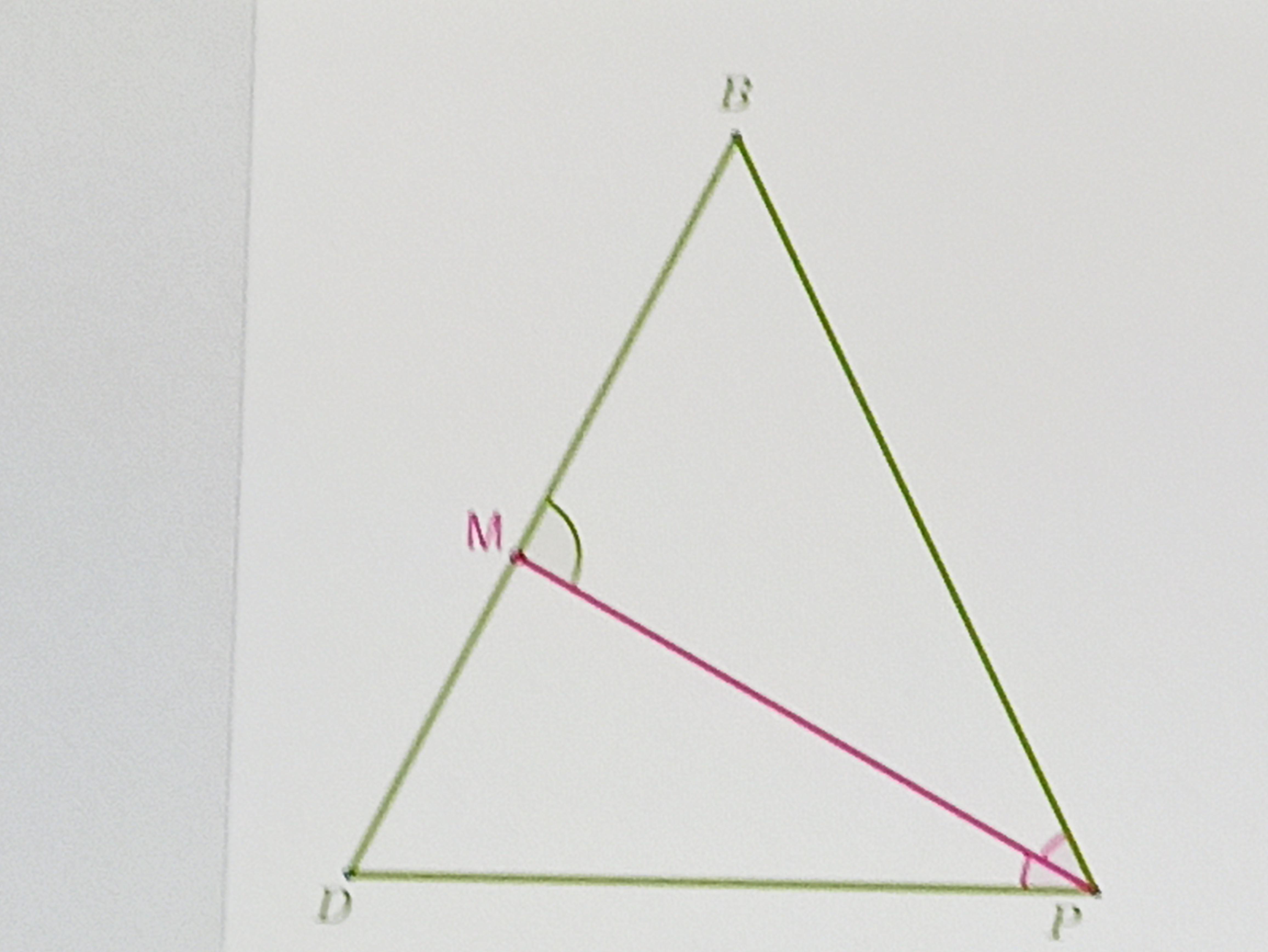
равнобедренном треугольнике DBP проведена биссектриса PM угла P у основания DP,∡PBM=78°, Определи величины углов данного треугольника

Answer 1

Пошаговое объяснение:

угол D = углу Р (т.к. треугольник DBP - равнобедренный)

угол D = (180°-78°)÷2 = 51°

Ответ: 51°;51°

Answer 2

Ответ:

∡PBM=78°, ∡BDP=∡BPD=51°

Пошаговое объяснение:

∡PBM=78°, а так как DBP - равнобедренный, то ∡BDP=∡BPD=(180°-78°) : 2 = 51°