решите системы неравенства.
⌗фото в закрепе.
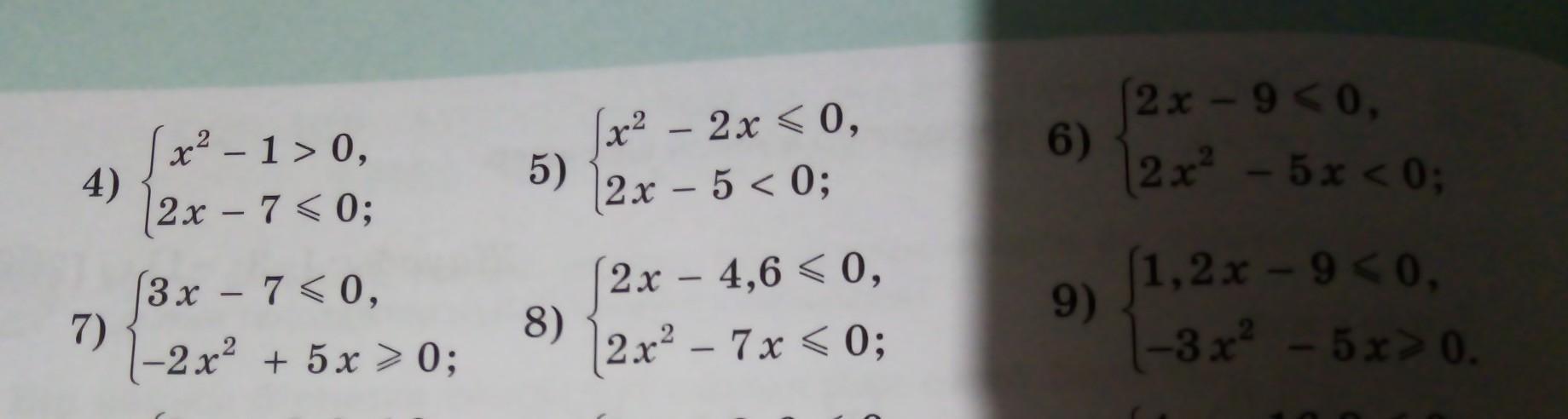
Ответы
Ответ:
В решении.
Объяснение:
Решить системы неравенств.
4) х² - 1 > 0
2x - 7 <= 0
Первое неравенство:
Приравнять к нулю и решить квадратное уравнение:
х² - 1 = 0
х² = 1
х = ±√1
х = ±1;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = -1 и х = 1.
у > 0 (график выше оси Ох) от -∞ до х = -1 и от х = 1 до +∞.
Решения неравенства: х∈(-∞; -1)∪(1; +∞).
Неравенство строгое, скобки круглые.
Второе неравенство:
2x - 7 <= 0
2х <= 7
x <= 7/2
x <= 3,5;
Решения неравенства: х∈(-∞; 3,5].
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда под круглой скобкой.
-∞//////////////////-1_________1////////////////////////////////////////////////////////+∞
-∞\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\3,5__________________+∞
Решения системы неравенств: х∈(-∞; -1)∪(1; 3,5], пересечение (двойная штриховка).
5) х² - 2х <= 0
2x - 5 < 0
Первое неравенство:
Приравнять к нулю и решить квадратное уравнение:
х² - 2х = 0
x(x - 2) = 0
x₁ = 0;
x - 2 = 0
x₂ = 2;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = 0 и х = 2.
y <= 0 (график ниже оси Ох) при х от х = 0 до х = 2.
Решения неравенства: х∈[0; 2].
Неравенство нестрогое, скобки квадратные.
Второе неравенство:
2x - 5 < 0
2х < 5
x < 5/2
x < 2,5;
Решения неравенства: х∈(-∞; 2,5).
Неравенство строгое, скобки круглые.
-∞____________________0//////////////2______________________+∞
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\2,5______________+∞
Решения системы неравенств: х∈[0; 2], пересечение (двойная штриховка).
7) 3х - 7 <= 0
-2x² + 5x >= 0
Первое неравенство:
3х - 7 <= 0
3x <= 7
x <= 7/3;
Решения неравенства: х∈(-∞; 7/3].
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда под круглой скобкой.
Второе неравенство:
-2x² + 5x >= 0
Приравнять к нулю и решить квадратное уравнение:
-2x² + 5x = 0/-1
2х² - 5х = 0
2х(х - 2,5) = 0
2х = 0
х₁ = 0;
х - 2,5 = 0
х = 2,5;
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х = 0 и х = 2,5.
у >= 0 (график выше оси Ох) при х от х = 0 до х = 2,5.
Решения неравенства: х∈[0; 2,5].
Неравенство нестрогое, скобки квадратные.
-∞\\\\\\\\\\\\\\\\\\\\0\\\\\\\\\\7/3_____2,5______________________+∞
-∞___________/////////////////////////////_______________________+∞
Решения системы неравенств: х∈[0; 7/3], пересечение (двойная штриховка).
8) 2х - 4,6 <= 0
2x² - 7x <= 0
Первое неравенство:
2х - 4,6 <= 0
2x <= 4,6
x <= 4,6/2
x <= 2,3;
Решения неравенства: х∈(-∞; 2,3].
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда под круглой скобкой.
Второе неравенство:
2x² - 7x <= 0
Приравнять к нулю и решить квадратное уравнение:
2x² - 7x = 0
2х(х - 3,5) = 0
2х = 0
х₁ = 0;
х - 3,5 = 0
х₂ = 3,5;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = 0 и х = 3,5.
y <= 0 (график ниже оси Ох) при х от х = 0 до х = 3,5.
Решения неравенства: х∈[0; 3,5].
Неравенство нестрогое, скобки квадратные.
-∞/////////////////////////////////0//////////2,3_________3,5____________+∞
-∞ _________________ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\_____________+∞
Решения системы неравенств: х∈[0; 2,3], пересечение (двойная штриховка).