Предмет: Алгебра,
автор: candycrash50
Решите уравнение пожалуйста
Приложения:
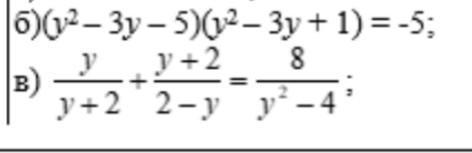
Ответы
Автор ответа:
1
Объяснение:
б)
Пусть y²-3y-5=t ⇒
Ответ: y₁=0, y₂=3, y₃=-1, y₄=4.
в)
ОДЗ: у+2≠0 у≠-2 у-2≠0 у≠2.
Ответ: y ∈ ∅.
BlackFox2030:
Добрый вечер! Можете пожалуйста помочь с алгеброй?
Автор ответа:
0
Решим первое уравнение методом замены .
Корней нет
Похожие вопросы
Предмет: Русский язык,
автор: маша1300
Предмет: Русский язык,
автор: lenyaaverin78
Предмет: Українська мова,
автор: Yurbass
Предмет: Русский язык,
автор: sounaly
Предмет: Русский язык,
автор: kol3130