Question

срочно 4 задание очень нужна помощь ​

Answer 1

Ответ:

Перпендикуляр РВ равен 2 см.

Объяснение:

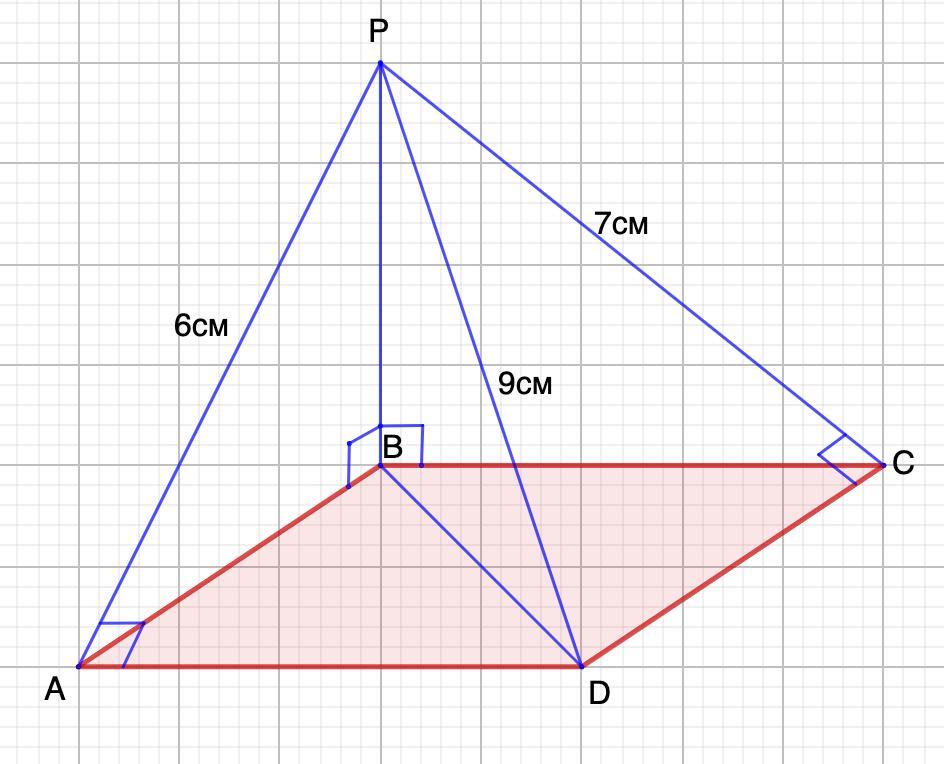
Найти расстояние РВ.

Дано: ABCD - прямоугольник;

Расстояние от Р до AD = 6 см;

Расстояние от Р до CD = 7 см;

PD = 9 см.

Найти: РВ.

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

Воспользуемся теоремой о трех перпендикулярах:

• Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Так как ABCD - прямоугольник, то

AB ⊥ AD ⇒ PA ⊥ AD.

Аналогично

РС ⊥DC.

1. Рассмотрим ΔAPD - прямоугольный.

По теореме Пифагора найдем AD:

AD² = PD² - AP² = 81 - 36 = 45

AD = √45 = 3√5 (см)

2. Рассмотрим ΔDPC - прямоугольный.

По теореме Пифагора найдем СD:

СD² = PD² - СP² = 81 - 49 = 32

СD = √32 = 4√2 (см)

3. Рассмотрим ΔАВD - прямоугольный.

По теореме Пифагора найдем ВD:

ВD² = АD² + АВ² = 45 + 32 = 77

ВD = √77 (см)

4. Рассмотрим ΔРDВ - прямоугольный.

По теореме Пифагора найдем РВ:

РВ² = PD² - BD² = 81 - 77 = 4

РВ = √4 = 2 (см)

Перпендикуляр РВ равен 2 см.