Предмет: Алгебра,
автор: sofianaumchak
СРОЧНО ПЖ ПЖ ПЖ!!!!!!
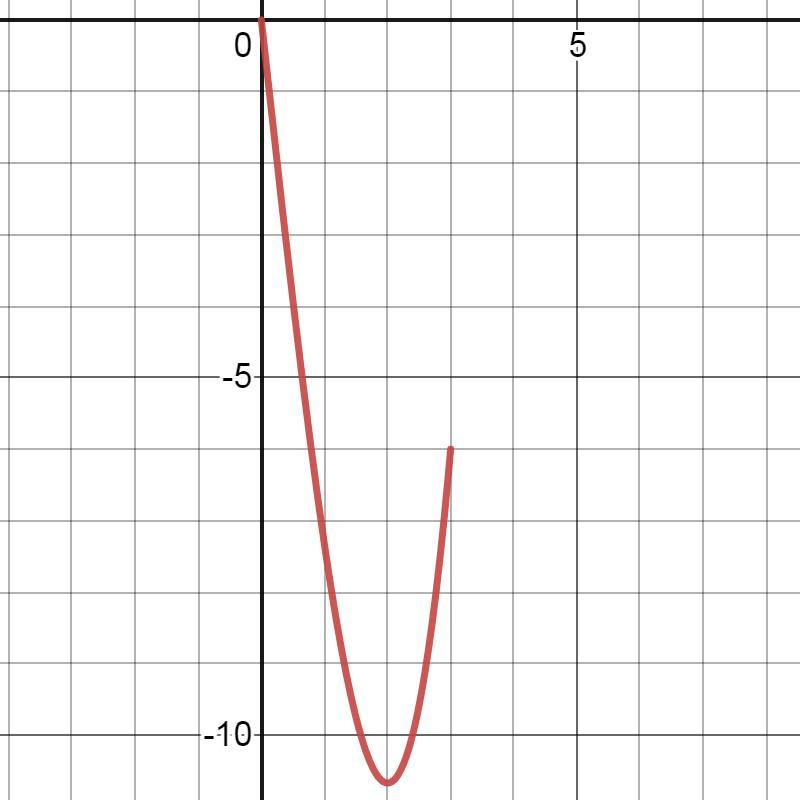
Обчисліть найбільше значения функції f(x)=(2x³/3) -8x на проміжку [0;3]
Ответы
Автор ответа:
2
Объяснение:
Ответ: f(0)=0=yнаиб.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: shimp
Предмет: Английский язык,
автор: vilenaVK
Предмет: Английский язык,
автор: мага256
Предмет: Окружающий мир,
автор: Erbolkizinurai
Предмет: Математика,
автор: Аноним