Предмет: Геометрия,
автор: 1234563434343
Помогите 100 баллов Геометрия
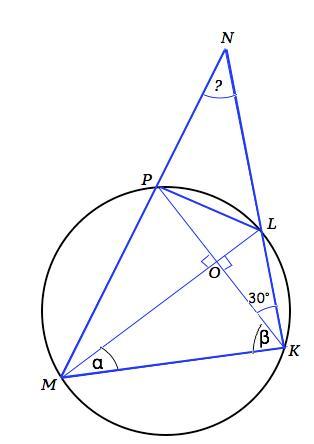
Дана окружность, пересекающая стороны MN и NK треугольника MNK в точках P и L. Вершины M и K этого треугольника лежат на данной окружности. Угол между отрезками ML и PK равен 90°, а угол PKN равен 30°. Найдите угол MNK.
Ответы
Автор ответа:
9
Ответ: 30°
Объяснение:
Вписанные ∠РМL и ∠РКL опираются на одну хорду РL и стягивают одну дугу ⇒ они равны по свойству вписанных углов. ⇒ ∠РМL=∠PKL=30°.
По условию ML⊥PK, поэтому ∆ МОК - прямоугольный. Примем острые углы этого треугольника равными α и β , тогда α+β=180°-90°=90°. Соседние им углы равны по 30°( доказано выше). Поэтому в ∆ МNК ∠NМК+∠NKM= α+β+2•30°=90°+60°=150°.
Из суммы углов треугольника искомый ∠MNK=180°-150°=30°
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Сима1ё
Предмет: Українська література,
автор: Флоравей
Предмет: Русский язык,
автор: недофизик4
Предмет: Литература,
автор: serafima2007k
Предмет: Физика,
автор: kurkak