Предмет: Геометрия,
автор: yulenkachernova
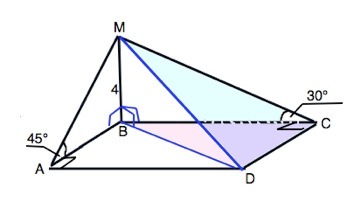
Из точки М проведен перпендикуляр МВ , равный 4 см, к плоскости прямоугольника АВСD.Наклонные МА и МС образуют с плоскостью прямоугольника углы в 45º и 30º соответственно.
а) докажите, что треугольники МAD и MDC прямоугольные;
б) найдите стороны прямоугольника;
в) докажите, что треугольник ВDС является проекцией треугольника МDС на плоскость прямоугольника, и найдите его площадь.
Ответы
Автор ответа:
123
а)
ABCD - прямоугольник. МВ перпендикулярна плоскости АВСD.
МА - наклонная, АВ - ее проекция. АВ⊥АD.
По т.о 3-х перпендикулярах МА⊥AD ⇒ ∆ МАD- прямоугольный.
МС - наклонная, – ВС её проекция.
По т.о 3-х перпендикулярах МС⊥СD – ∆ МСD- прямоугольный. ч.т.д.
б)
АВ=МВ:tg45°=4:1=4 (см)
ВС=MB:tg30°=4:(1/√3)=4√3
CD=AB=4; AD=BC=4√3
в)
MD - наклонная, BD - её проекция.
ВС - проекция наклонной МС.⇒
∆ BDС - проекция ∆ MDС на плоскость АВСD.
S∆ BCD=BC•CD:2=4√3•4:2=8√3 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Zaira8085
Предмет: Қазақ тiлi,
автор: rcxhijj
Предмет: Окружающий мир,
автор: polena55915
Предмет: Литература,
автор: arr767
Предмет: География,
автор: intertorg