Предмет: Алгебра,
автор: wwwwl
решить методом подстановки
Приложения:
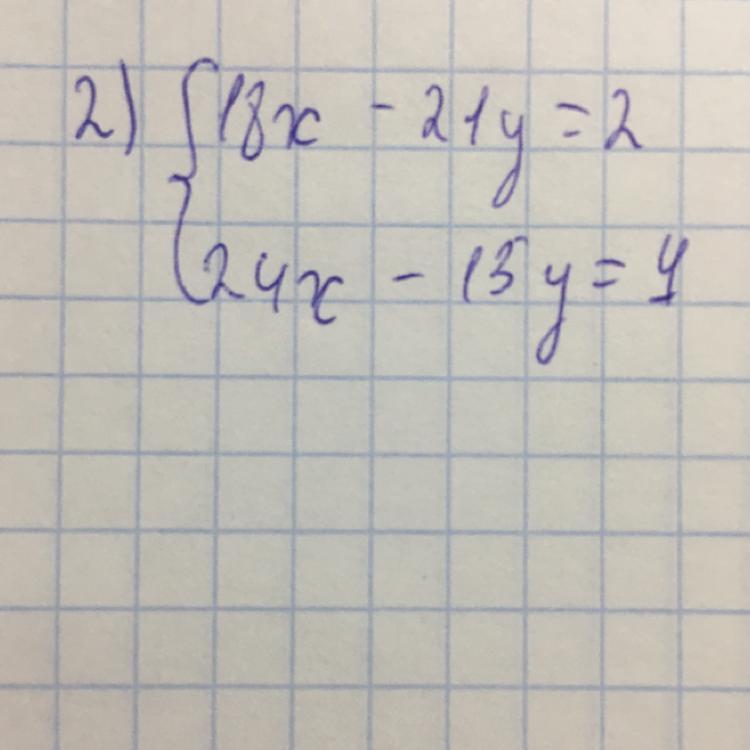
Ответы
Автор ответа:
1
Решаем второе уравнение:
;
;
;
;
;
8 + 39y = 12;
39y = 4;
y =
Возвращаемся в систему:
Решим первое уравнение:
x = ;
x = ;
x = ;
x = ;
x = =
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: dasoalalalagfgg
Предмет: Қазақ тiлi,
автор: бибинур4
Предмет: Русский язык,
автор: Никнейм1337
Предмет: Другие предметы,
автор: elekovao
Предмет: Физика,
автор: masnaoksana14