Question

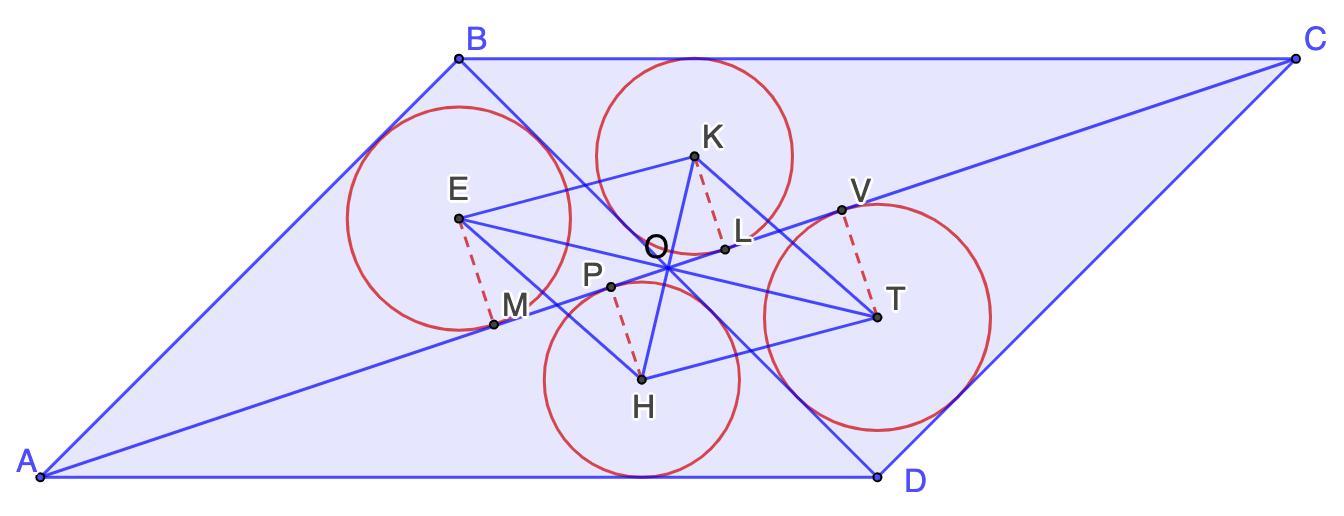
Диагонали разбивают параллелограмм на 4 треугольника докажите что центры окружностей вписанных в эти треугольники образуют ромб с рисунком

Answer 1

Ответ:

Доказано, что ЕКТН - ромб.

Объяснение:

Диагонали разбивают параллелограмм на 4 треугольника докажите что центры окружностей вписанных в эти треугольники образуют ромб.

Дано: ABCD - параллелограмм.

AC и BD - диагонали.

Окр.Е, Окр.К, Окр.Т, Окр.Н - вписанные в ΔABO, ΔOBC, ΔCOD, ΔAOD соответственно.

Доказать: ЕКТН - ромб.

Доказательство:

1. Рассмотрим ΔВОС.

Центр вписанной окружности лежит на биссектрисе угла.

⇒ ОК - биссектриса ∠ВОС.

∠COD - внешний.

ОТ - биссектриса (Окр.Т - вписанная)

Биссектриса внешнего угла треугольника перпендикулярна биссектрисе внутреннего угла, смежного с ним.

⇒ КО ⊥ ОТ.

2. Рассмотрим ΔВОС и ΔAOD.

• Диагонали параллелограмма точкой пересечения делятся пополам.

⇒ АО = ОС; ВО = OD.

• Вертикальные угла равны.

⇒ ∠ВОС = ∠AOD (вертикальные)

ΔВОС = ΔAOD (по двум сторонам и углу между ними, 1 признак)

Аналогично ΔАВО = ΔOCD.

Формула для нахождения радиуса вписанной окружности:

$\displaystyle r=\frac{2S}{a+b+c}$,

где S - площадь треугольника, а  a, b, c - стороны треугольника.

• В равных треугольниках равны соответственные элементы.

⇒ радиусы вписанных окружностей тоже равны.

⇒ VT = ME; KL = HP.

3. Рассмотрим ΔМЕО и ΔOTV - прямоугольные.

VT = МЕ (п.2)

∠ЕОМ = ∠TOV (вертикальные)

ΔМЕО = ΔOTV (по катету и острому углу)

⇒ ЕО = ОТ (как соответственные элементы)

4. Рассмотрим ΔLKО и ΔHPO - прямоугольные.

LK = PH (п.2)

∠KOL = ∠HOP (вертикальные)

ΔLKО = ΔHPO (по катету и острому углу)

⇒ KО = ОH (как соответственные элементы)

5. Рассмотрим ЕКТН.

ЕО = ОТ; KО = ОH (п.3; п.4)

• Если в четырехугольнике диагонали точкой пересечения делятся пополам, то это параллелограмм.

⇒ ЕКТН - параллелограмм.

• Если у параллелограмма диагонали перпендикулярны, то он является ромбом.

КО ⊥ ОТ или КН ⊥ ЕТ. (п.1)

⇒ ЕКТН - ромб.