Предмет: Алгебра,
автор: sufyanivemil2007
решите уравнение......
Приложения:
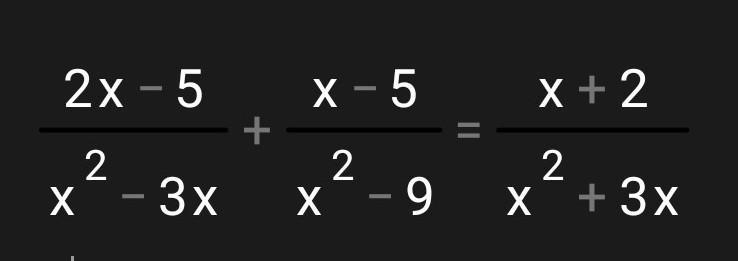
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: tusy87
Предмет: Русский язык,
автор: egortepaev
Предмет: Английский язык,
автор: karina00000009
Предмет: Алгебра,
автор: 76501023
Предмет: Қазақ тiлi,
автор: mosya94