Предмет: Алгебра,
автор: levon2111
Помогите решить срочно отдам все балы
Приложения:
Ответы
Автор ответа:
1
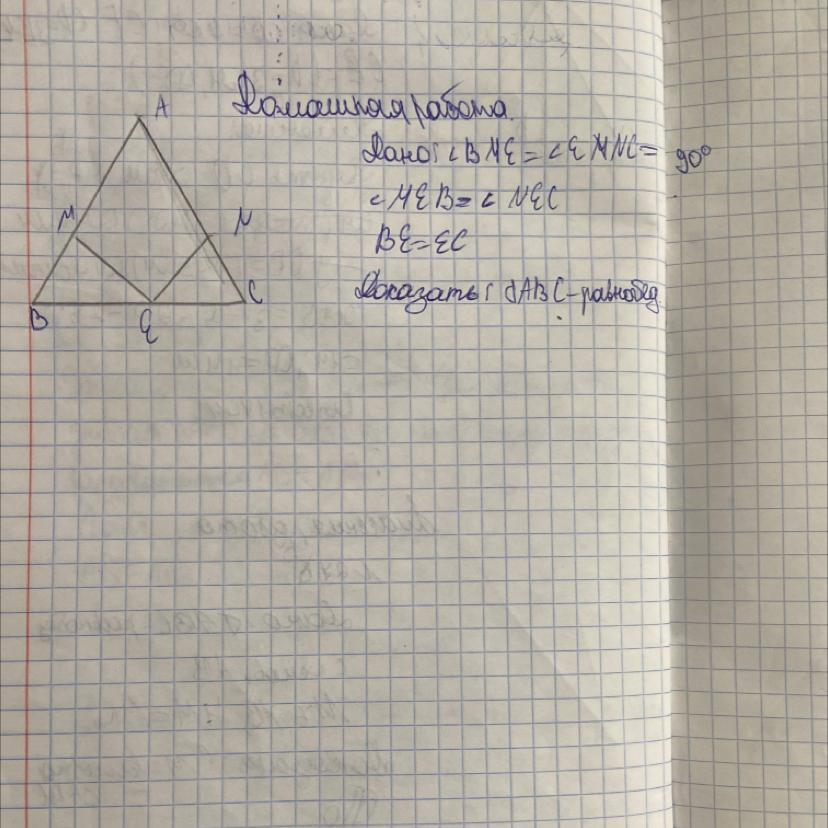
Рассмотрим Δ BME и Δ ENC :
< BME = < ENC = 90⁰ - по условию
Значит эти треугольники прямоугольные .
< MEB = < NEC - по условию
Гипотенузы BE и EC равны по условию
Значит Δ BME = Δ ENC - по гипотенузе и острому углу
Из равенства треугольников следует равенство углов B и C в треугольнике ABC .
Но если в треугольнике углы при основании равны , то этот треугольник равнобедренный .
Δ ABC - равнобедренный . Что и требовалось доказать .
Автор ответа:
0
Объяснение:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
ΔВМЕ=ΔСNЕ, значит ∠В=∠С, а ΔАВС - равнобедренный, т.к. углы при основании ВС равны.
Доказано.
Похожие вопросы
Предмет: Английский язык,
автор: груша3
Предмет: Русский язык,
автор: камиль75
Предмет: Окружающий мир,
автор: zhernovkova05
Предмет: Математика,
автор: marinaakyla
Предмет: Алгебра,
автор: Микаса8999