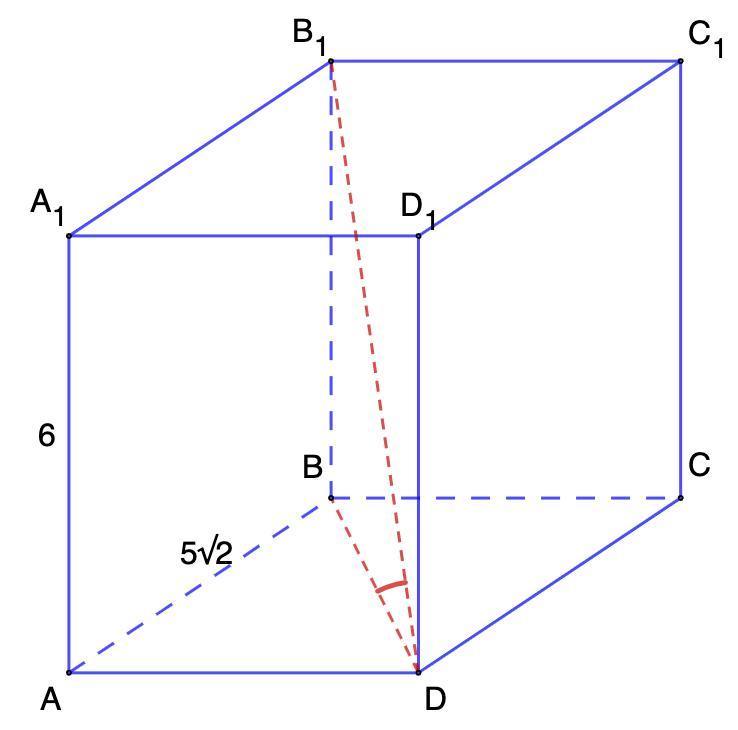
ПОМОГИТЕ!!! Можно пожалуйста с рисунком и решением!!

Ответы
Ответ:
Тангенс угла между B₁D и АВС равен 3/5
Площадь полной поверхности призмы равна 220√2 ед.²
Объяснение:
Требуется найти тангенс угла наклона BD₁ к плоскости АВС; площадь полной поверхности призмы.
Дано: ABCDA₁B₁C₁D₁ правильная призма;
АВ = 5√2; АА₁ = 6.
Найти: Тангенс угла между B₁D и АВС; Sполн.
Решение:
- В основании правильной четырехугольной призмы лежит квадрат.
1. Определим угол между B₁D и АВС.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
⇒ искомый ∠BDB₁.
2. Рассмотрим ΔABD - прямоугольный.
По теореме Пифагора:
BD² = AB² + AD² = 50 + 50 = 100
BD = √100 = 10
3. Рассмотрим ΔВВ₁D - прямоугольный.
- Тангенс угла - отношение противолежащего катета к прилежащему.
4. Найдем площадь полной поверхности призмы.
Sполн. = Sбок. + 2Sосн.
Sбок. = Р (ABCD) · h, где Р (ABCD) - периметр основания, h - высота призмы.
Sосн. = а² , где а - сторона квадрата.
Найдем площадь боковой поверхности:
Sбок. = АВ · 4 · АА₁ = 5√2 · 4 · 6 = 120√2
Площадь основания:
Sосн. = АВ² = 50
Площадь полной поверхности призмы:
Sполн. = 120√2 + 50 · 2 = 220√2
Площадь полной поверхности призмы равна 220√2 ед.²